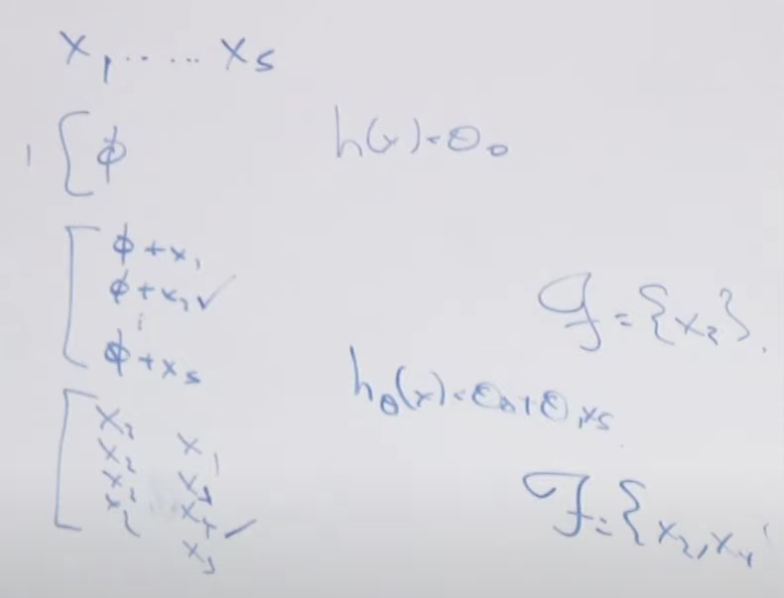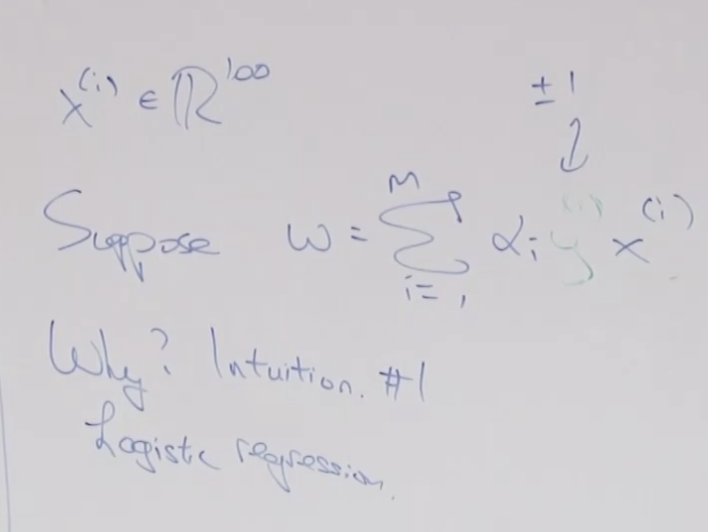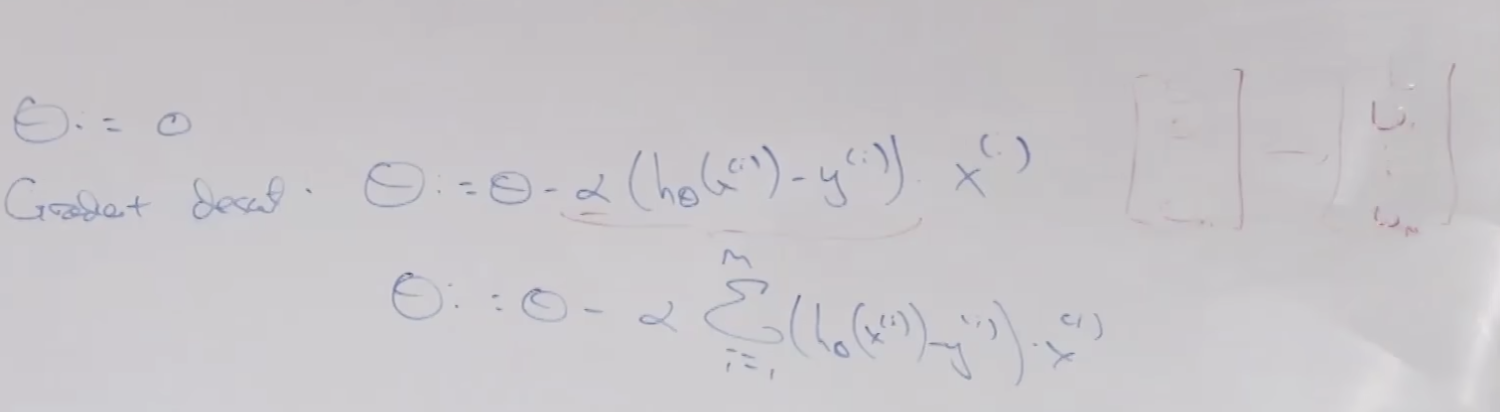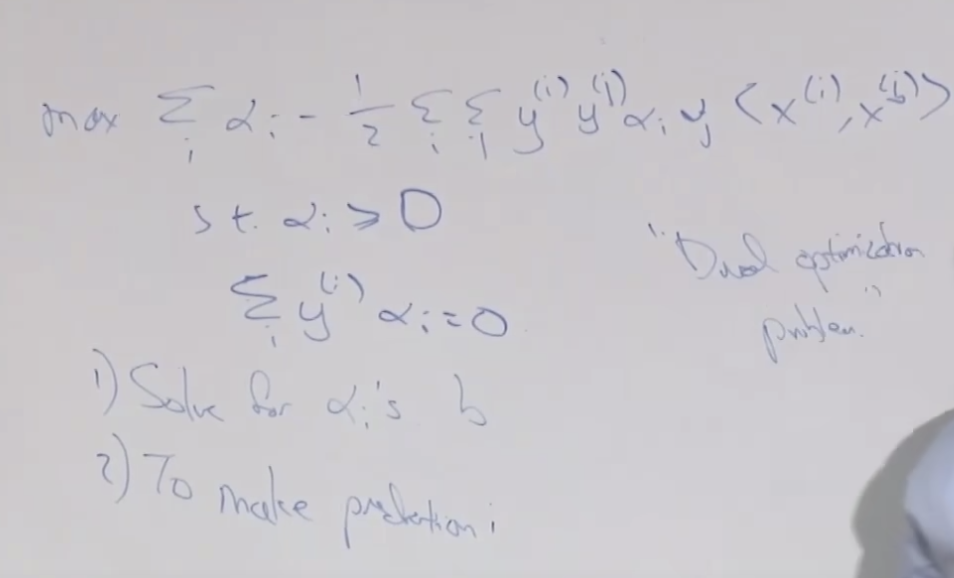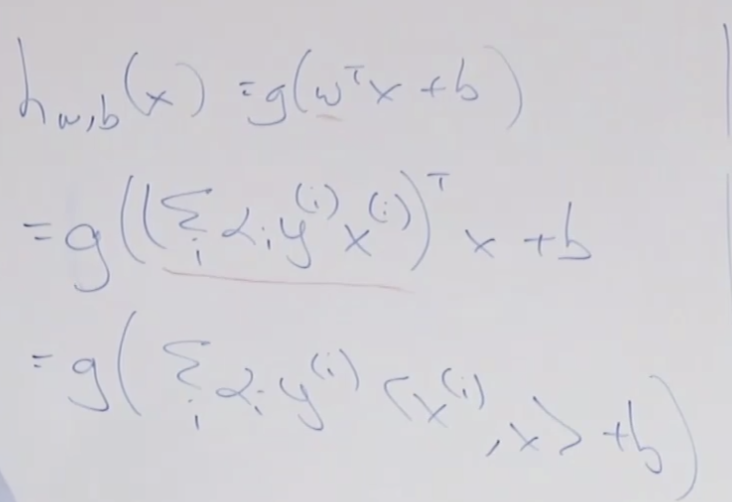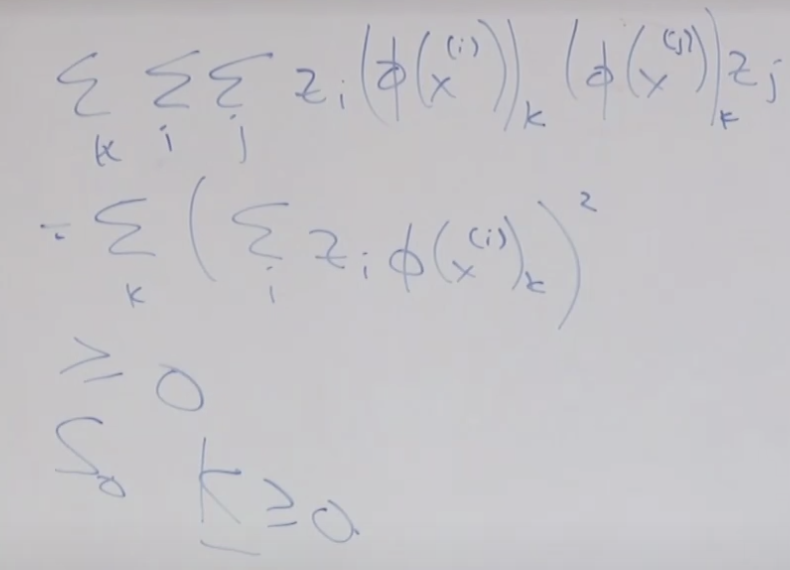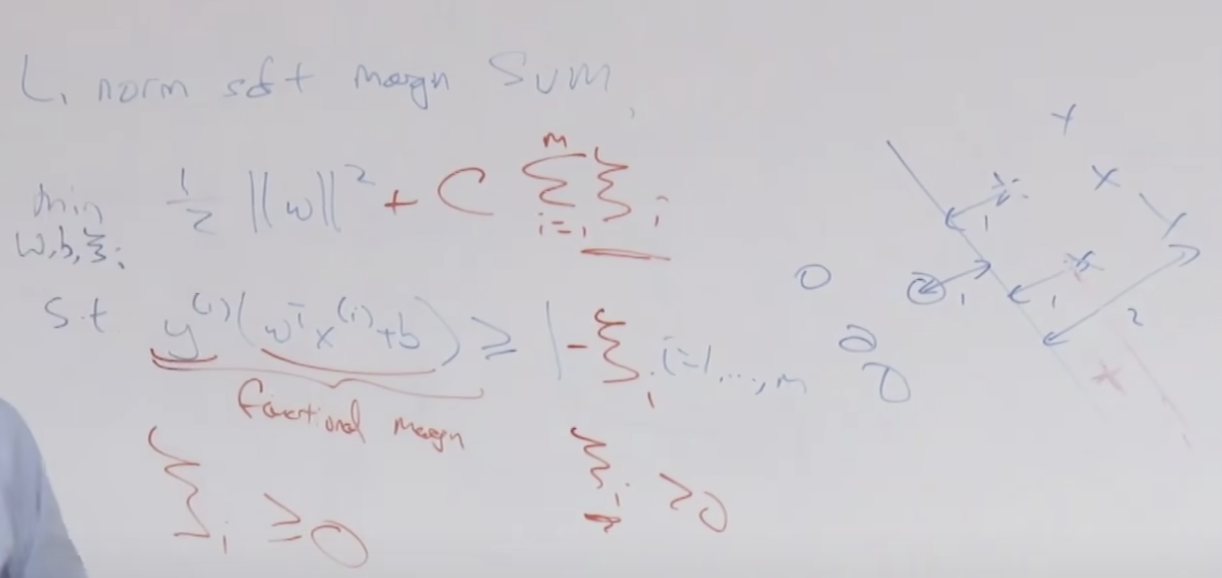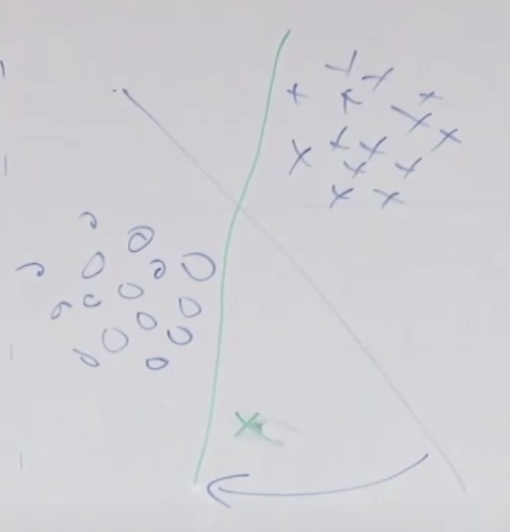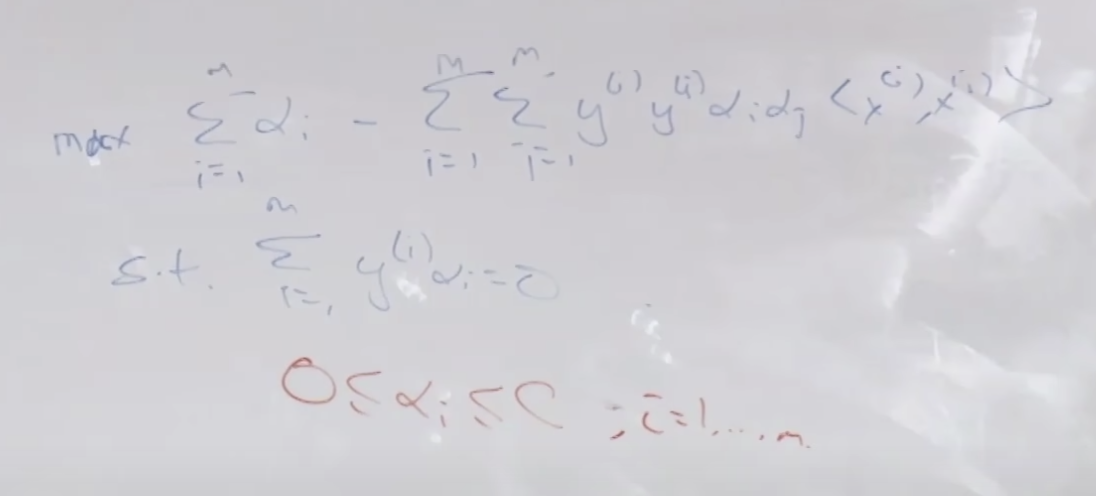Lecture 8 - Data Splits, Models & Cross-Validation | Stanford CS229: Machine Learning (Autumn 2018)
주요내용
- Bias/ Variance
- Regularization 정규화
- Train/dev/test splits
- Model selection & Cross validation
Bias/ Variance
이전 강의에서 예를 들었던 주택 사이즈별 가격 데이터를 가지고 이야기 해 보겠습니다. 같은 데이터를 가지고 아래와 같이 3가지의 모델을 만들 수 있습니다. 왼쪽은 언더피팅(underfit)된 1차원 모델의 High bias 그래프이고 가운데는 적당한 2차원 모델, 오른쪽에는 다중 선형모델로 오버피팅(Overfitting)된 모델의 High Variance 그래프 입니다.

Regularization 정규화
아래는 로지스틱 회귀 공식 입니다. - 부호 뒤의 람다|| ||^2가 Regularization 내용입니다. 이 변수를 통해 곡선의 구부러진 정도를 조정할 수 있습니다.

λ람다에 따른 곡선의 변화를 보면 아래와 같습니다. λ가 아주크면 0에 가까워지는 군요.

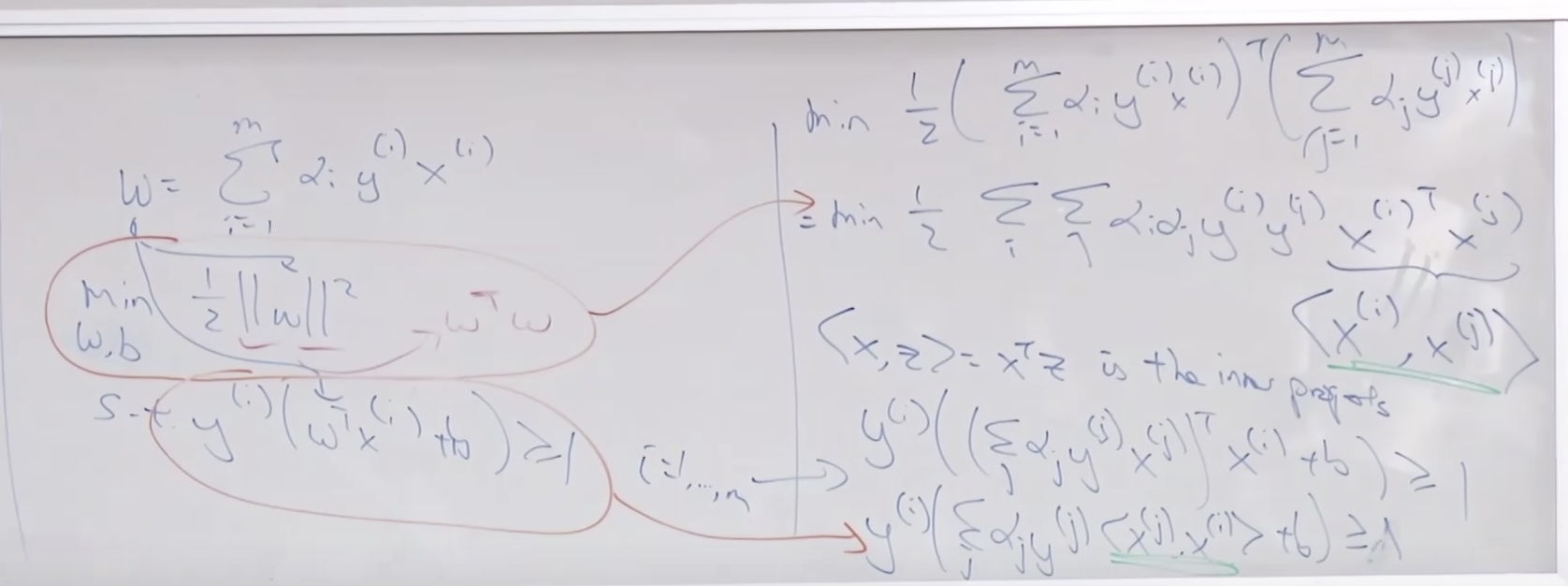
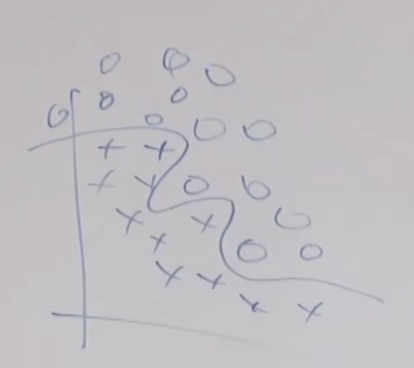
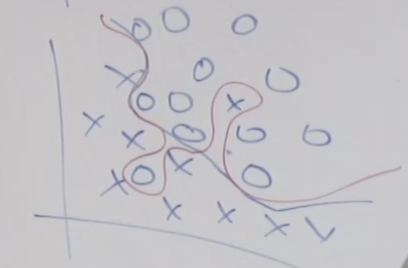
SVM의 경우 수많은 변수를 세타함수를 통해서 만들어 사용하는 데(고차원 매핑) 왜 오버피팅이 되지 않을 까요? 그것은 - λ||θ||^2 와 같은 역할을 하는 것이 SVM에서는 minimize ||w||^2 때문에 결국 같은 효과 즉 오버피팅을 막는 효과가 있습니다.
나이브 베이즈의 예를 들어 보겠습니다. 전 시간에 예를든 스팸 분류기도 좋고 트위터 데이터에 대한 감성분석도 좋습니다. 이러한 분류 문제를 다룬다고 할때 특히 이렇게 피처는 많고(10,000) 예제 데이터는 적을때(100)는 로지스틱 회귀에 정규화 Normalization 을 추가하여 개발한 모델의 성능이 나이브 베이즈 보다 좋습니다. 정규화를 이용하지 않으면 오버피팅되기 때문에 성능이 좋지 않습니다. 보통은 피처가 예제 데이터 보다 10배이상 크면 정규화를 이용합니다.
정리하면

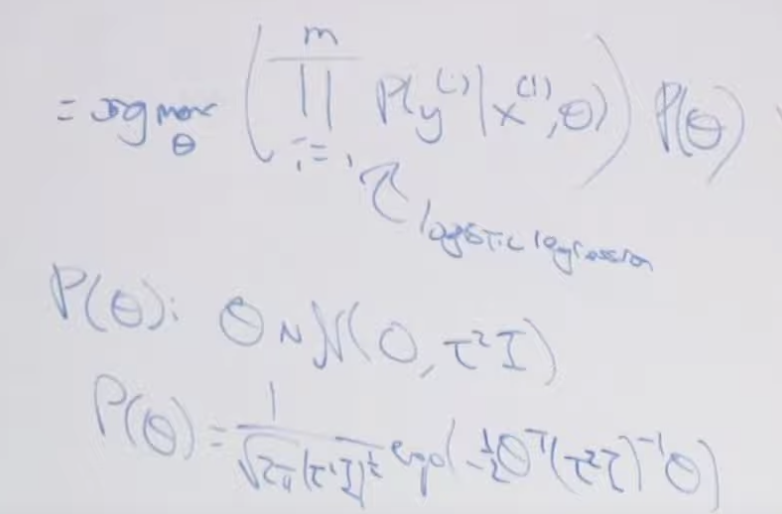
Frequentist와 Bayesian 학자들 사이의 차이점에 대해서 설명합니다. Frquentist는 MLE를 구하고 베이지안 학자는 MAP(Maximization A Posteriori)를 구합니다.
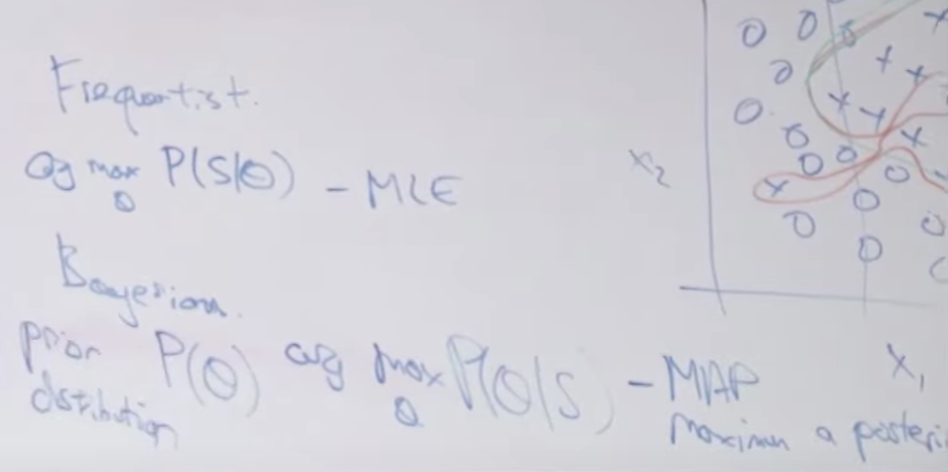
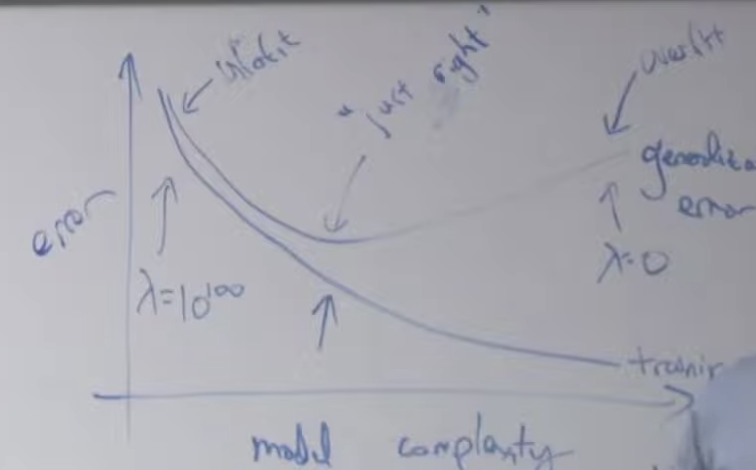
y축은 에러율, x 축은 모델의 복잡도를 기준으로 그래프를 그려보면 아래와 같습니다. 일반적인 그래프는 모델 복잡도가 낮으면 언더핏되고 모델 복잡도가 높아질 수록 점점 에러가 줄어들게 됩니다. 그러다가 중간이 지나면 다시 에러율이 상승하는데 이렇게 상승된 상태의 모델을 오버피팅된 모델이라고 합니다. 곡선이 위로 꺽기기 시작하는 중간지점이 가장 좋은 모델 복잡도를 가진(에러가 가장 낮은) 모델입니다.
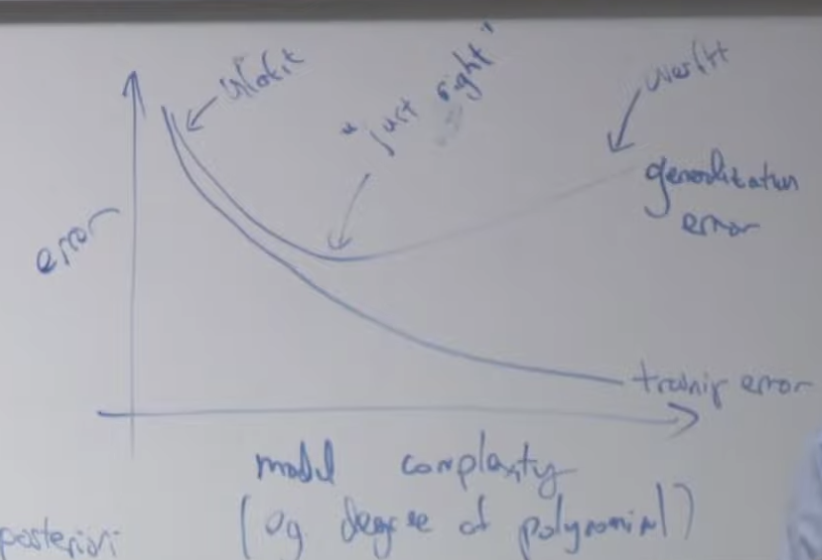
여기에 정규화(Normalization)을 위해 λ를 사용할 경우 λ크기에 따라 에러의 변화를 만들 수 있습니다. λ가 너무 크면 제일 왼쪽 처럼 언더피팅되고 λ를 0으로 설정하면 (정규화를 안하면) 오른쪽 처럼 오버피팅됩니다. 적당한 λ값을 설정해주면 중간에 가장 에러가 낮을때를 만들 수 있습니다.
Train/dev/test splits
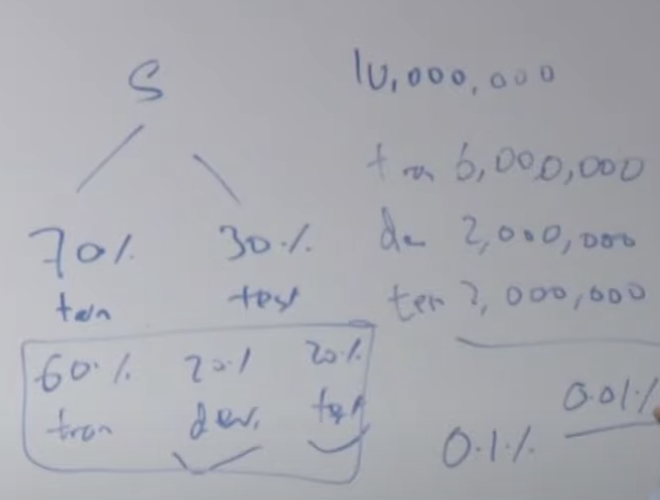
일반적으로 트레인/개발/테스트로 나눕니다. 트레인/검증/테스트(Train/Validation/Test) 로도 불립니다. 10,000 개의 example 데이터가 있을 경우 모델의 복잡도를 하나씩 높여가면서 결과를 보고, 또는 람다 값 등 변수들을 조정하면서, 그리고 정규화를 적용해 보면서 모델을 만듭니다.

이때 데이터셋(S)를 train용 dev용, test용 으로 분리합니다. dev 는 development를 말합니다.
각각의 모델을 S(train) 테레인 데이터를 가지고 훈련하여 적당한 하이퍼파라메타를 찾습니다.
옵션으로 논문 페이퍼를 위한 내용 필요시 테스트 데이터를 가지고 사용합니다. 이전에는 한번도 사용되지 않은 데이터 입니다.

degree를 높여가면서 S(dev)개발용 데이터를 이용한 에러가 아래 왼쪽처럼 감소하다가 증가하는 degree가 나옵니다. 보기에는 4.9에러가 나온 degree의 모델을 사용하면 될 것 같은데 자세히 보면 그전, 그리고 전전 에러율이 5.0, 5.1로 큰 차이가 없습니다. 이러한 경우에 실제 모델 degree의 차이때문에 생긴 에러 차이가 아니라 바이어스나 모델의 다른 변수에 의한 것일 수 있습니다. S(test)로 측정해서 선택하도록 합니다.

예전에는 대부분 데이터 셋(S)은 아래처럼 70%와 30%로 나누거나 60%, 20%, 20%로 나누었습니다. 그런데 예제 데이터가 10,000,000개 있을 경우 6:2:2로 분리하는 것이 좋을까요? 정말 test 데이터가 2,000,000개 필요한지 생각해 봐야합니다. 온라인 추천이라든가 매우 작은 소수점아래 자리까지 고려하는 경우에는 많은 test 데이터가 필요합니다. 그러나 다른 업무에서는 이렇게 많이 필요하지 않을 수 있습니다. 데이터가 충분히 많이 있다면 90%:5%:5%로 나누는 것이 좋습니다. 그리고 여기에 원하는 정확도의 차이(0.01%까지 고려해야하는지 0.0001%까지 고려해야하는지) 에 따라서 dev/test 수를 조정하면 됩니다.
Model selection & Cross validation
이처럼 데이터를 트레인/데브/테스트로 분리하는 것을 (Simple) Hold-out cross validation 이라고 합니다. 그리고 dev set은 Cross Validation Set 이라고도 불립니다.
그럼 데이터 셋이 작은 경우에는 어떻게 할까요? 예를 들면 m=100 개 셈플이 있다면 70개를 훈련에 30개를 개발(검증)에 써야합니다. 훈련과 검증에 너무 작은 수 입니다.

이러한 경우 K-fold Cross Validation을 이용합니다. k는 임의 의 숫자인데 통상적으로 10을 씁니다. 여기서는 설명을 위해 5로 합니다. 전체 데이터셋(S)를 K로 나눈 숫자만큼의 덩어리로 만들어서 , k번 반복하는 동안 한번에 한 덩어리 데이터를 가지고 훈련하는 방법입니다. K 번 훈련해서 나온 에러를 평균해서 하나의 degree(복잡도, 하이퍼 파라메터)에서의 에러율을 구합니다. 이런 절차를 degree 숫자만큼 반복하면서 진행하면 어느 degree에서 가장 작은 에러가 발생하는 지 알수있습니다. (측, 최적의 degree모델을 찾을 수 있습니다.) 데이터를 가지고 1번의 훈련과 검증이 가능 했던 것을 k 번 반복할 수 있게되어서 훈련을 더 잘할 수 있습니다. 알고리즘은 아래의 오른쪽에 나와있습니다.

옵션으로 해도되고 안해도 되는데, 이렇게 해서 선택하게된 degree의 모델을 가지고 전체 100% 훈련데이터를 가지고 훈련해서 모델을 만들 수 있습니다.
이러한 Cross Validation 은 특히 적은 데이터를 가지고 있을때 유용합니다.
Leave-one-out Cross Validation
훈련 데이터의 개수가 아주 적을 때(100보다 같거나 작을 경우) Leave-one-out Cross Validation을 쓰면 좋습니다. 예를 들어 훈련 데이터가 20개(m=20)일 경우의 예를 들면 데이터들을 아주 작게 즉 1개 단위로 사용할 수 있게 분리해서 사용 하는 방법입니다. 즉, 20개로 분리하고 19개를 훈련에 사용하고 1개로 검증하고, 전에 사용했던 훈련 데이터중 하나를 검증으로 사용하고 나머지를 모두 훈련데이터로 사용하는 방법입니다. 이렇게 하면 모델의 훈련과 검증을 20번 할 수 있습니다. 컴퓨팅에 많은 비용이 소모되므로 데이터가 많을 경우는 사용하지 않습니다. 말씀 드린 대로 100개 이하인 경우만 사용을 권장합니다.

Feature Selection

피처 선택(Feature Selection)은 여러 개의 피처 중에서 성능에 많은 영향을 미치는 피처들을 찾는 것을 말합니다. 전방 피처 선택(Forward Feature Selection)과 후방 피처 선택(Backward Feature Selection) 방법이 있습니다. 전방 피처 선택의 예를 들면 5개의 피처가 있다고 가정할 때 가장 영향력이 큰 피처를 하나씩 추가해 가는 방법입니다. 아래의 경우 x2가 제일 중요한 피처라고 발견된 경우 x2는 고정하고 추가로 x2와 x1, x2와 x3, x2와 x4, x2와 x5 처럼 x2피처에 하나의 피처를 추가할 경우 어떤 피처가 가장 영향력이 큰지를 찾는 방법입니다. 이러한 방법으로 하나씩 피처를 선택해나가는 방법이 전방 피처 선택법(Forward Feature Selection)입니다.