스탠포드 기계학습/머신러닝 강의 Lecture 6 - Support Vector Machines | Stanford CS229: Machine Learning (Autumn 2018)
주요 내용
- Naive Bayers(나이브 베이즈)
- - Laplas Smooding
- - EV models
- Comment on apply ML
- SVM Intro
Recap
나이브 베이즈는 Generative 알고리즘으로 텍스트 분류나 트위터 메세지 같은 것은 분류할 수 있습니다.
텍스트를 사전에 정의된 순서에 따라 있는지 없는지를 표시하는 방법(원핫 인코딩)으로 하나의 문서(메일 또는 메시지)를 표시할 수 있습니다. 그래서 X에 있는 각 단어가 이메일에서 발견될 확률을 계산하여 전체 X의 확률을 구했습니다.

이것을 확률 공식(나이브 베이즈)으로 정리하면 아래와 같았습니다.

p(x|y) y일 때 x가 (정규분포에서) 나타날 확률과 p(y) 전체 y(스펨 or 정상) 메일이 (0 또는 1이므로 베르누이 분포에서) 나타날 확률을 결합하여 계산합니다.
p(x|y)는 각 xj 요소의 확률들의 곱으로 계산할 수 있습니다.
필요한 파라메타들은 p(y=1) = Φy 1(스팸)인 메일이 나올 확률
p(xj = 1 | y=0) = Φj | y=0 0(정상)인 메일에서 xj가 나올 확률
p(xj = 1 | y=1) = Φj | y=1 1(스팸)인 메일에서 xj가 나올 확률
Φ 는 최대가능도법(MLE)를 통해 아래와 같이 구할 수 있습니다.

이렇게 해서 정리된 파라메타들과 입력값을 이용하여 새로운 데이터 입력시 예측을 할 수 있습니다.

NIPS 라는 학회에 참여하기위해 준비하는 메일을 받았다고 합시다. 관련된 단어수는 6017개 라고 하시죠. 문제는 이 단어들이 기존에 학습될때 사용되지 않은 단어이기 때문에 확률을 계산하면 0으로 나옵니다. 이 건 매우 않 좋은 현상입니다. 한번도 못봤던 단어라고 해서 그 단어가 포함될 확률이 0이라고 하기에는 무리가 있습니다.

그래서 라플라스 스무딩이라는 기법을 사용합니다.
라플라스 스무딩
라플라스 스무딩을 먼저 설명하고 다시 돌아오겠습니다. 그래서 다른 예를 살펴 보시지요.
팀의 경기 승패를 예측한다고 생각해 봅시다. 12/31일에는 이길까요? 질까요? (0은 패, 1은 승을 표시 합니다.)

x=1일(승리할) 확률은 아래와 같이 구할 수 있습니다. 전체 1의 갯수 나누기 전체갯수(1과 0의 갯수의 합)를 하면 됩니다.

다음 경기를 승리할 확률이 없습니다. 즉, x = 1일 때 확률이 0입니다. 4번 연속해서 패배했다고 이길 확률이 아예 없다(0)는 건 좀 잘못된 것 같습니다. 실제로도 가끔 이기는 경우가 생기기 때문에 잘못된 계산 같습니다.
그래서 이러한 경우 우리는 라플라스 스무딩이라는 것을 할 수 있는데요. 이것은 각 경우의 수에 1을 더해주는 것입니다. 0의 갯수 4에 1을 더해주고, 1의 갯수 0에 1을 더해주어서 분모나 분자에 0을 안만드는 방법입니다.

이렇게 하니 1/6이 나와서 0보다는 좋아 보입니다.
수학자 라플라스가 라플라스 스무딩을 만든 이유에 대해서도 설명해주십니다. 재미있네요. 태양은 매일 뜨지만 내일 아침 태양이 뜰 확률이 정말 1인(확실한)가? 혹시 모를 우주나 은하계의 충돌이나 사건으로 인해 태양이 안 뜰 수도 있는데 확실하다고 하는 것은 잘못된 것 아닌가라는 관점에서 그럼 이런 것을 어떻게 정의하면 좋을까를 생각해서 나온 것이라고 합니다.
일반화 해서 쓸때는 분모에 요소수(k)를 사용하네요.

다시 나이브 베이즈로 돌아가서, 공식에 라플라스 스무딩을 적용해 보면 아래와 같습니다. 클래스가 2개라서 분모에 2를 더했네요.

이 알고리즘의 장점은 간단하다는 것 입니다. 카운트만해서 계산하면 확률을 구할 수 있습니다.
일반화된 예를 보겠습니다. 이를 위해 예전에 예시를 들었던 주택 예시를 들어보겠습니다. 주택이 30일 내에 팔릴지 안팔릴지를 판단하는 모델을 만든다고 가정합시다. 입력 데이터로 방 크기를 버켓팅(Bucketing)하여 아래과 같이 구분하여 입력합니다. 이렇게 하면 이전에 (스팸메일분류모델에서는) 베르누이 분포였지만 여기서는 다항 분포 확률이 됩니다.

그리고 보통 버켓팅은 10개의 구간으로 한답니다. 이처럼 데이터를 변형하면 나이브 베이즈를 여러 문제에 적용해서 사용할 할 수 있습니다.
텍스트 분류에 더 좋은 모델을 설명 드리겠습니다. 1만개의 단어가 있는 사전을 기준으로 아래의 텍스트를 인코딩 해보면 아래와 같습니다.

이와 달리 새로운 표현(New Representation) 방법에 대해서 알아봅니다. 사전이 중심이 아니라 입력 데이터가 중심이 되서 입력 데이터의 단어를 사전에서 단어가 나오는 순서로 표현하는 것 입니다.

데이터를 표현하는 백터가 매우 작아지네요..
그래서 전에 사전을 기준으로 존재여부 (0,1)을 표시했던 방법을 Multi-variate Bernoulli Event Model이라고 합니다.

나중에 새로운 표현법으로 설명한 방법은 Multinomial Event Model이라고 합니다.

이름이 비슷하여 혼동될 수 있습니다.
새로운 표현방법 Multinormial event model을 이용하여 나이브 베이즈 공식을 정리하면 아래와 같습니다. 예전에 스펨메일 분류시와 유사하지만 조금 다릅니다. j가 1부터 n까지 반복되는데 스펨메일에서는 10,000번 반복했고 여기서는 메일의 단어수 만큼만 반복하면 됩니다. 그리고 여러 카테고리가 있기 때문에 카테고리별로 단어 xj가 해당 카테고리에 속할 확률을 구합니다. Φk | y=0 = p(xj=k | y= 0)

y=1 스팸일때의 Φ 공식은 아래와 같습니다. 이 확률을 최대로 높이는 가능도(MLE)를 구합니다. 그리고 빨간색으로 표시된 것 처럼 라플라스 스무딩을 적용해 줍니다. 분모에 10,000이 더해졌는데 이것은 사전에 들어있는 단어숫자 입니다.

사전에 없는 단어가 나오면 어떻게 처리할까요?
두가지 방법이 있는데 하나는 그냥 무시하고 단어를 사용하지 않는 것이고요, 다른 하나는 UNK(Unknown Tocken)이라는 특별 기호로 매핑하여 적용하는 방법입니다.
일반적으로 나이브 베이즈는 로지스틱 회귀 보다 정확도 성능이 낮아서 잘 안씁니다. 그러나 나이브 베이즈는 반복 작업이 필요없어서 빠르고 몇줄 안되는 코딩으로 쉽게 개발 할 수 있는 장점이 있습니다.
해결해야할 ML 문제를 직면했을 때 빠르게 지저분한 코드를 만들어보는게 좋습니다. 이런 경우 나이브 베이즈는 매우 좋은 툴입니다.
소프트웨어를 개발할때 한꺼번에 10,000 라인의 코드를 입력하고 컴파일하지 말고 여러개의 모듈로 만들어서 각 모듈 하나씩을 만들고 단위 테스트해 나가는 방법이 더 좋은 소프트웨어 개발 방법입니다. 모델 개발할때도 마찬가지로 일단 빠르게 지저분한 코드라도 돌아가는 것을 만들어 놓고 시작하는 것이 좋습니다. 그런 다음 어떤 부분이 정확도를 떨어트리는지를 파악하고 하나씩 해결해가면서 성능을 높일 수 있습니다.
GDA와 나이브 베이즈는 일반적으로 다른 로지스틱 회귀나 딥러닝 모델에 비해 정확도 성능이 낮습니다. 그럼에도 불구하고 간단하고 속도가 빠른 장정들 때문에 모델 개발 초기에 이러한 알고리즘을 가지고 빠르게 작동하는 모델을 만드는 것은 좋은 접근 방법 입니다.
나이브 베이즈의 단점으로 아빠, 엄마와 같이 비슷한 단어를 구분하지 않습니다. 그냥 단어의 출현을 가지고 활용하게 되는 것이지요. 워드 임베딩이라는 다른 테크닉이 있는데 이것은 이런 문제를 해결하는 방법입니다. 즉, 단어간의 유사성이 모델 훈련시 학습됩니다.
SVM Support Vector Machine
SVM은 아래 그림에서처럼 복잡한 결정 경계(Decision boundary)를 만들 수 있는 모델입니다. 로지스틱 회귀와 같은 선형모델에서는 그림에 그려진 직선처럼 구분 할 수 밖에 없는데 이것에 비하면 SVM은 정말 잘 분류 합니다.

사실 입력값 x1, x2만 사용하지 말고 x1과 x2를 이용해서 다른 입력값을 만들수 있는데 (이것이 그림 하단에 있는 Φ(x)처럼 x1*x2를 한다든가, x1^2 등 새로운 값을 만들어내는 것입니다.) 이 만들어진 피처를 이용해서 로지스틱 회귀를 훈련하면 초록색과 같이 복잡한 경계도 분류할 수 있습니다. 문제는 x1, x2에서 다양한 피처 X를 만들어 내는 것이 힘든일이라는 것이지요 그리고 어떤 피처가 적합한지 알 수 없기 때문에 어려운 작업입니다.
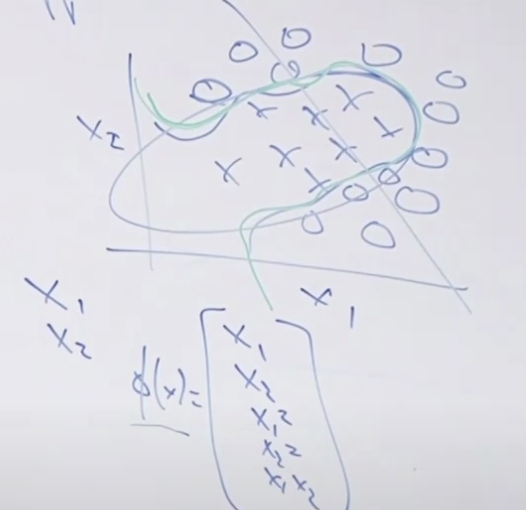
SVM이 딥러닝 보다 성능이 더 좋지는 않습니다. 그래도 많이 쓰이는 이유는 턴키(Turn Key)이기 때문입니다. 무슨 말이냐하면 많은 패키지에서 이미 SVM이 잘 만들어져 있어서 (key를 넣고 돌리면되는 것처럼) 그냥 가져다 쓰면 쉽게 만들 수 있습니다.
앞으로 진행할 내용은 아래와 같습니다.
* Optimal margin classifier : 선형분리와 비슷하지만 살짝 다른 부분이 있습니다. 일단은 그냥 로지스틱 회귀와 같은 것으로 가정하겠습니다. 아래에 설명 할 예정입니다.
* (다음 시간에) Kernels. 커널이 자동적으로 무한대에 해당하는 피처를 생성해 줍니다.
* (다음 시간에) Inseparable case
Functional margin
아래의 윗 부분의 내용은 로지스틱 회귀입니다.

Geometry margin
빨간색과 녹색의 두가지 모델이 있다고할때 어떤것이 더 좋은 모델일까요? 잘은 모르지만 녹색이 좋은 모델 같습니다. 왜그럴까요?

그 이유는 경계선과 요소간의 거리가 먼 것이 더 잘 분리했습니다. 그래서 두 모델 모두 100% 잘 분류하는 모델이 더라도 녹색 모델이 더 좋은 모델입니다. 이렇게 Geometric margin을 기준으로 경계를 분리할 수 있습니다. 기본적인 SVM은 이 경계마진을 이용하여 분리선을 만듭니다.

SVM관련 표기법입니다. 1 또는 -1을 반환하는 함수네요.

로지스틱 회귀와 SVM 함수 공식을 비교하여 아래에 보여줍니다.
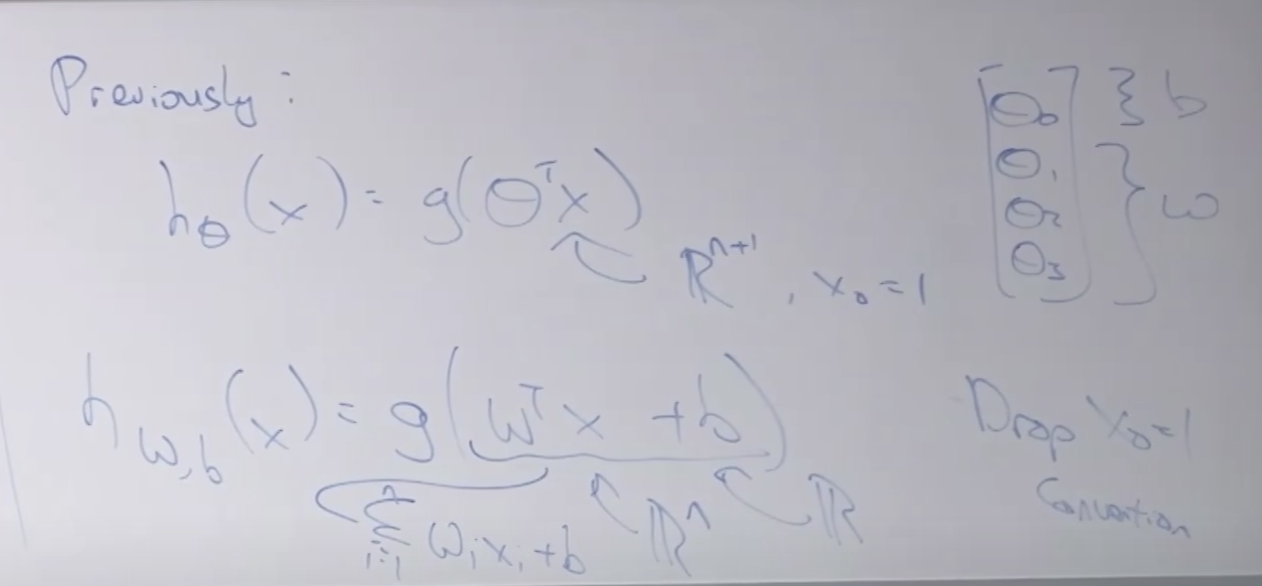
하나의 하이퍼플레인(선) 을 결정하는 functional margin 계산 방벙을 설명합니다.


정규화를 이용해서 functional margin의 치팅을 막을 수 있습니다.

Geometric margin 을 아래와 같이 구할 수 있습니다. 유클리디안 거리를 가지고 선과 점의 거리를 계산할 수 있겠네요

Functional margin과 비교해 봅니다.


최적화 시키는 공식 입니다. 이것도 convex optimization problem 이라고 합니다.
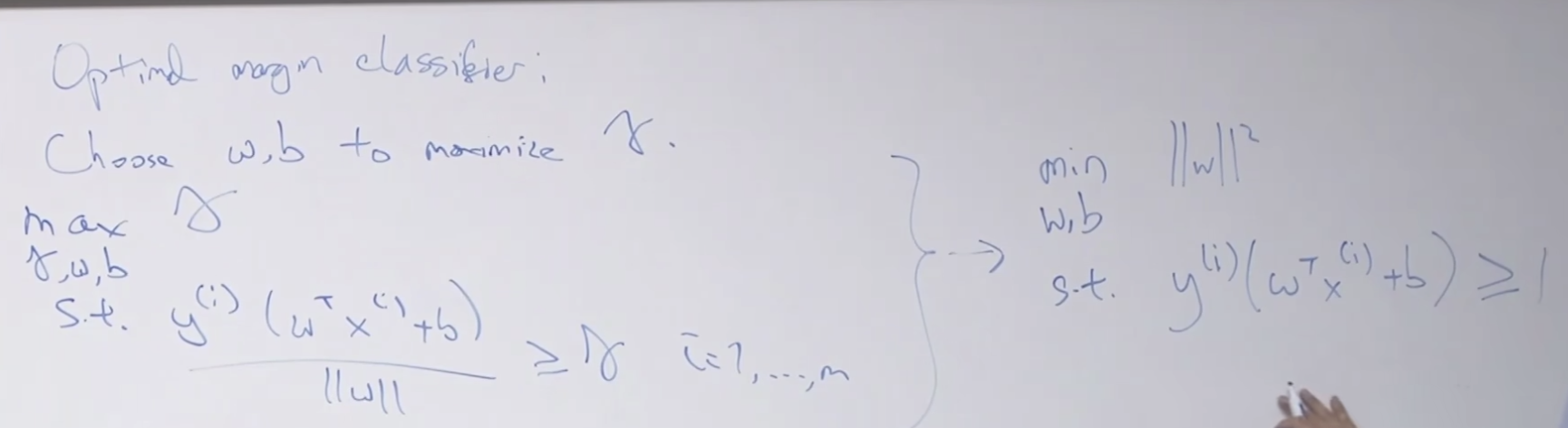
공식에 대한 상세 풀이라든가 설명이 있는 강의 노트가 없어서 조금 아쉬운 부분도 있네요. 그래도 전체적인 개념과 구조를 이해할 수 있습니다.
SVM은 매우 성능이 좋은 알고리즘 입니다. 딥러닝이 나오기 전까진 말이죠. 그정도로 성능이 좋고 빠름니다. 그래서 최근에도 많이 쓰이는 알고리즘 입니다.
게다가 턴키 알고리즘으로 사용하기도 쉽습니다. ^^
아래는 해당 강의 동영상 입니다.
https://www.youtube.com/watch?v=lDwow4aOrtg&list=PLoROMvodv4rMiGQp3WXShtMGgzqpfVfbU&index=6