Lecture 10 - Decision Trees and Ensemble Methods | Stanford CS229: Machine Learning (Autumn 2018)
주요 내용
- Decision trees 의사결정 나무
- Ensemble Methods 앙상블 방법
- Bagging 배깅
- Random Forests 랜덤 포레스트
- Boosting 부스팅
Decision Trees 의사결정 나무
시간(월)과 위도를 가지고 스키를 타기 좋은지 아닌지를 구분하는 분류기를 만든다고 생각해 봅시다. 데이터를 통해 가능한 지역과 시간에 +를 표시하고 불가능한 지역과 시간에 -를 표시하면 아래와 같습니다.
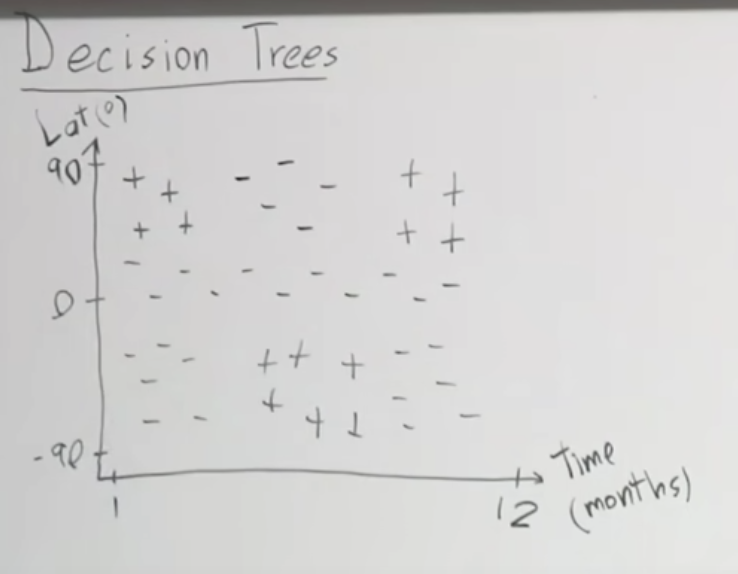
Greedy top-down recursive partitioning
모든 케이스들을 측정한다는 측면에서 Greedy하다고 할 수 있고, 전체 데이터를 가지고 분류해나가기 때문에 top-down 이라고 말할 수 있습니다. 그리고 데이터를 분류하고 나서 분류된 한 부분을 가지고 다시 분류하기 때문에 recursive 하다고 말할 수 있습니다.
첫번째는 위도가 30도 인지를 가지고 분류할 수 있습니다. 그래서 위도가 30보다 큰 지역과 작은 지역으로 나누어 집니다. 이어서 두번째로는 시간(월)을 가지고 분류할 수 있습니다. 3월보다 작은 달인지 아니닌지로 구분합니다. 이렇게 나누어진 그림이 아래와 같습니다.
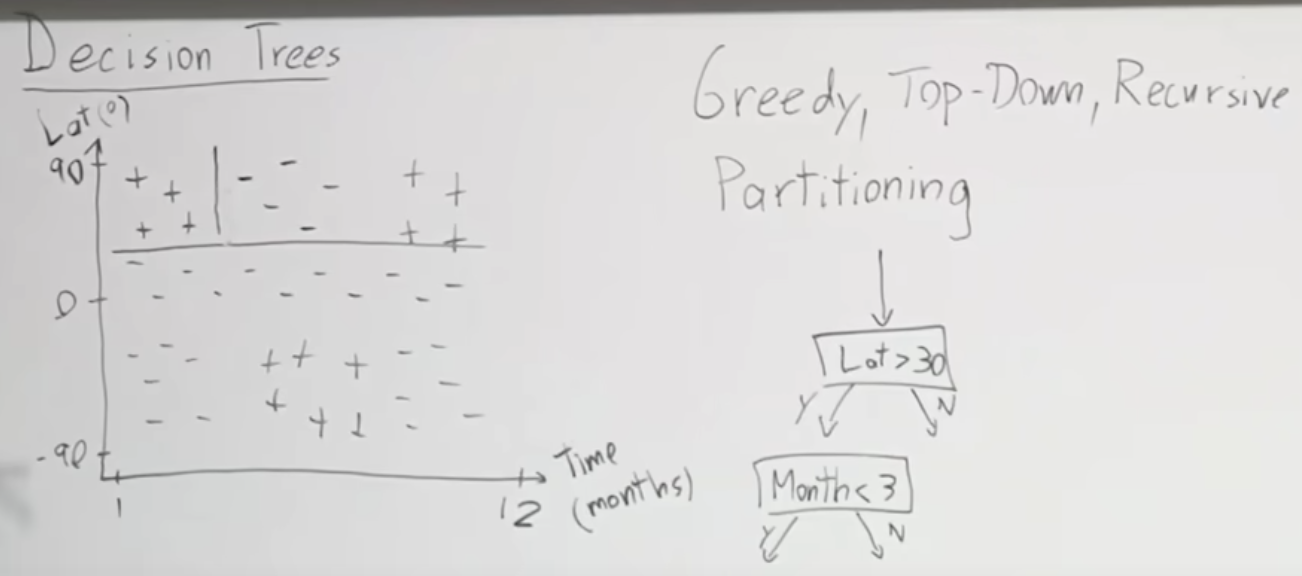
이러한 방법으로 계속 분류를 하면 아래와 같이 분류할 수 있습니다.

아래는 p(positive, +) 지역(Region Rp)을 찾는 것을 함수 Sp로 만들었을때의 공식입니다. 입력 변수로 j는 피처를 나타내고 t는 임계값을 의미합니다. Rp는 Region parent 즉, 상위/부모의 지역을 말합니다. 아래 공식을 설명해보면 j 에 해당하는 Xj 값이 임계값 t 보다 작을 때는 첫번째 지역 R1에 할당하고, 크거나 같을 경우 두번째 지역 R2에 할당합니다.

그럼 분류 후 얼마나 틀렸는지를 계산하는 로스는 어떻게 계산할 까요?


그런데 잘못 분류한 로스 계산에 문제가 있습니다. 아래 두 그림에서 처럼 실제로 다르게 분류를 했음에도 불구하고 로스는 오른쪽에 보이듯이 좌우 모두 100 입니다. 심지어 부모 노드의 로스 L(Rp)도 100으로 같습니다.

그래서, 이런 문제를 해결하기 위해 단순 로스가 아닌 크로스 엔트로피 로스(Cross-entropy loss)를 사용하게 됩니다.
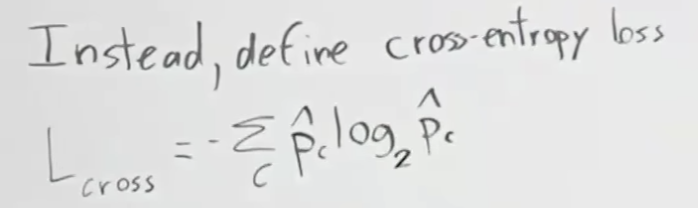
크로스 엔트로피 로스는 L(R1)과 L(R2)의 평균에 해당하는 지점에서 곡선과 직각이되는 점-L(Rp)와의 차이(Gain)를 계산하는 것 입니다. 아래에서 Change in loss로 적혀 있는 부분이 Gain입니다. 즉, 부모 노드에서 발생한 로스 보다 자식 노드 2개에서 발생한 로스의 평균이 더 적게 되는 경우 입니다.

이것은 Gini 값이라고 해서 아래와 같이 정의된 값도 많이 쓰입니다.

아래는 잘 못 분류된 경우를 설명하는 그림입니다. 부모 노드의 로스(L(Rp))가 결국 자식 노드 2개의 평균과 같은 것이 되버리기 때문에 자식 도드에서는 의미 없는 분류를 한 것과 같습니다.

Regression Trees
이번에는 Regression Trees에 대해서 알아보도록 하겠습니다. Decision Trees의 예로 사용했던 스키 예를 이용하겠습니다. 다만 적합한지 아닌지 + - 로 구분했던 것을 적설량으로 구분하는 예를 들어보겠습니다. Decision Tree에서와 같이 위도와 시간 월에 따른 위치에 적설량을 숫자로 표시합니다. 그리고 이것을 잘 분류하게 됬을 경우 아래처럼 구분하는 선들이 그려지게 됩니다.

지역 Rm에 해당하는 예측값 y^m을 수식으로 나타내면 아래와 같습니다. 이것은 지역 Rm에 있는 모든 수의 합을 숫자 갯수로 나누어서 계산하는 값으로 결국 지역의 평균 값이 됩니다.

로스는 스퀘어드는 MSE(Mean Squared Error)와 같이 각 예측 값에서 평균값(y^m)을 뺀값의 제곱을 누적하여 전체 갯수로 나누어서 구합니다.

Categorical Vars 를 가지고도 모델을 만들 수 있습니다. 그러나 9개의 카테고리가 있다고 만 가정해도 2^9만큼의 분리가능한 것들이 생겨서 너무 복잡하고 비효율적입니다.

왼쪽에 North, Equator, South로 카테고리를 분류 할 수 있습니다. 이는 특히 이진트리(Binary trees)의 경우도 적용할 수 있습니다. 각 분류의 갯수 별로 소팅한뒤에 숫자에 따라 분류해 나갈 수 잇습니다.

Regularization of Decisioon Trees
트리 모델을 모든 훈련데이터에 훈련 시키면 결국 모든 훈련케이스를 만족시키는 트리를 만들게 되어 결국 최종 결과가 하나씩 연결되는 Overfitting이 발생하게됩니다. 이를 방지하기위해 정규화가 필요한데 여기에 사용되는 다양한 휴리스틱 정규화 방법에 대해서 알아보면 아래와 같습니다. 최소 리프 사이즈를 제한 하거나, 트리의 깊이를 제한 하거나, 노드들의 최대 수를 정해 놓거나, 최소로 줄어드는 로스를 정해 놓거나, 검증 데이터에서 잘못 분류된 가지를 제거하는 등이 있습니다. 특히, min decrease in loss의 경우 부모노드 보다 자식노드가 최소 어느정도는 더 분류를 잘해야 하는 지를 정하는 방법으로, 데이터 피처의 중요도-잘 분류하는 데이터 피처에 따라서 위에서 아래로 정리되게 만드는 방법입니다.

Runtime
n은 예제수, f는 피처수, d를 나무의 깊이라고 하면, 테스트 시간은 O(d)가 되고 이때 깊이 d는 log2n 보다 작습니다. 여기서 log2n이 의미하는 것은 말 그대로 훈련 예제수에 로그를 취한 값 입니다. 다시 말하면 전체 예제수로 훈련해서 만들어진 훈련된 트리를 이용해서 테스트를 하게 되기 때문에 훈련에서 만들어진 트리의 깊이에 따라 속도가 달라지게되고 이 깊이는 훈련을 통해 잘 분리되도록 하는 이진트리(하위노드가 2개인 트리)를 만들었다고 할경우 결국 훈련데이터의 예제수에 로그를 취한 값이 보다 작아지게 됩니다. 리프 노드에 하나의 예제가 달린다고 최학의 경우를 가정한 것이 log2n입니다. 아무튼 너무 당연한 이야기 인데요 트리의 예측 속도는 트리의 깊이 만큼 비교해야하기 때문에 O(d)입니다.

그럼 훈련 시간은 어떻게 될까요? 각 포인트는 O(n) 속도의 노드에 속한 한 부분이고, 각 노드에서 포인트의 비용은 O(f)입니다. 이 말은 피처 f가 위도, 시간-월 이렇게 2개있을 경우 O(2) 만큼의 시간이 걸린다는 말입니다. 깊이 마다, 각 노드에서 피처마다 처리하는 시간이 필요하고 이런 계산을 예제수 만큼해야하니 모두 곱한 O(nfd)가 훈련 시간이 됩니다.
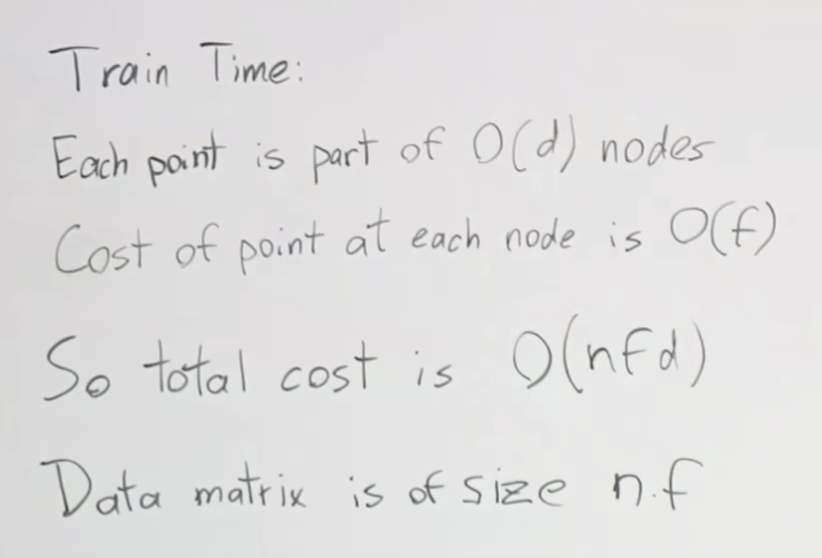
Downsides
이제 의사결정트리의 단점을 알아볼까요? 선형회귀로 간단히 분류가 가능한 +와 - 데이터 들이 있습니다. 그런데 이것을 의사결정나무 Decision Trees로 분류하게 되면 많은 분류 기준이 필요하여 복잡한 트리가 만들어 질 수 있습니다. 속도도 느려지고 잘 분류가 안되는 경우도 생길 수 있습니다.

요약- 장점/단점
의사결정나무의 장점과 단점은 아래와 같습니다. 장점으로는 먼저 설명하기 쉽습니다. 모르는 사람에게도 예를 들면 10개 질문을 통해서 분류한다고 설명할 수 있습니다. 모델을 해석하기 쉽고, 범주형 변수(Categorical Vars)에 유용하며, 속도가 빠릅니다. 단점으로는 분산이 큰 모델로 훈련 데이터에 오버피팅 되기 쉽습니다. 변수 사이에 상호작용이 작은 경우에 분석에 약하고(반대로 상호작용이 큰 경우에는 강합니다), 그리고 예측 정확도가 낮습니다.

Ensemble Methods 앙상블 방법

여기서 독립 가정을 제거하면 전체 모집단의 평균(X-bar)에 대한 분산은 아래와 같이 계산할 수 있습니다. 공식을 풀어서 이해해 보면 p 에 의해 연관된 x 샘플이 많을 수록 분산은 커지고 데이터수(n) 이 클수록 분산이 작아지게 됩니다.

이처럼 정확도를 높이기 위한 방법중 하나가 앙상블 ensemble이며 앙상블에는 다양한 방법이 있습니다.
다른 알고리즘을 쓸수 있고, 다른 훈련 데이터 셋을 사용할 수도 있습니다. 베깅과 부스팅이라는 기법도 있습니다. 베깅의 대표적인 예는 랜덤포레스트이고 부스팅의 대표적인 예는 에이다부스트(Adaboost)와 xGboost 입니다.

Bagging 배깅
베깅에 대해서 알아보면 다음과 같습니다. 배깅은 부트스트랩 에그리게이션(Bootstrap Aggregation)의 축약어 입니다. 실제 모집단 P에서 샘플 S를 뽑아서 훈련 셋을 사용합니다. 이때 우리는 샘플이 모집단과 같다고 가정하고 모델을 만듭니다. 여기에 부트스트랩이라는 기술을 추가하는데 이것은 샘플에서 다시 샘플을 추출하여 Z라는 샘플을 만들고 이것을 훈련에 이용하는 것을 말합니다.

이렇게 생성된 여러 개의 샘플 z를 가지고 모델 G를 여러번 훈련할 수 있고 그 결과를 평균할 수 있습니다. 이 부분이 바로 에그리게이션 Aggregation 파트에 해당하는 내용입니다. 즉, 여러 샘플 데이터 셋을 가지고 훈련한 모델의 여러 결과들을 합치는 부분입니다.

이 기술을 적용하면 바이어스와 베리언스(오차와 분산, Bias-Variance)에 변화를 주게 됩니다. 앞서 분산에 대한 공식을 정리한 것이 있는데 이것을 부스팅에 적용하면 아래와 같습니다. 즉, Var(x-)의 내용중 분모를 M (샘플z 수)로 바꾸어 준것 밖에 없습니다. 부스팅을 적용하면 공식에 있는 p를 줄입니다. 그리고 데이터가 많을 수록 분산을 줄입니다. 반면 오차는 살짝 올라 갈 수 있습니다.

의사결정트리는 높은 분산에 낮은 바이어스를 가지고 있기 때문에 배깅과 매우 잘 맞습니다. 배깅이 분산을 낮추어 주기 때문입니다.

Random Forests 랜덤 포레스트

Boosting 부스팅
부스팅은 배깅과 다르게 바이어스를 줄이는 효과가 있습니다. 변수 사이의 상효작용에 강합니다. 이 기술은 반복적인 모델 훈련을 합니다. x1, x2 피처를 가지고 분류 모델을 만든 다고 가정해 보시죠. 아래 왼쪽과 같이 분류모델을 만들어 분류를 할 수 있는데 빨간색 박스 처럼 오분류하는 경우가 발생합니다. 이러한 경우 다음 훈련에서 해당 예제 샘플의 가중치를 높혀서 훈련하면 오른쪽의 그림처럼 큰 +와 -를 만들수 있고 이들을 고려한 분류모델을 만들면 그림과 같이 위/아래로 나누는 분류선(모델)을 만들 수 있습니다. 이런 식으로 반복해 나가면서 모델을 학습하는 방법이 부스팅 입니다.


아래는 강의 링크 입니다.
https://www.youtube.com/watch?v=wr9gUr-eWdA&list=PLoROMvodv4rMiGQp3WXShtMGgzqpfVfbU&index=10