스텐포드 기계학습 강의 Lecture 4 - Perceptron & Generalized Linear Model | Stanford CS229: Machine Learning (Autumn 2018)
이번 강의 주요 내용
- Perceptron(퍼셉트론)
- Exponential Family(지수계열, 지수족)
- Generalized Linear Model(GLM, 일반화 선형 모델)
- Softmax Regression(Multiclass classification)소프트맥스 회귀
Perceptron
퍼셉트론을 배우는 이유는 지난 시간에 이어 분류 문제를 다루는 알고리즘 중에서 기본적이고 역사적으로 의미가 있는 알고리즘이기 때문입니다. 너무 간단하고 한계가 많아서 실제로 많이 사용되지는 않지만 이것이 기반이되어 최근에 많이 쓰이는 딥러닝이 발전되었기 때문에 퍼셉트론을 이해하는 것은 중요하다고 할 수 있습니다.
퍼셉트론에 대한 정의와 배경에 대한 이야기가 강의에서는 부족해서 이해하기 어려울 수 있습니다.
그래서 설명을 추가해 보았습니다.
위키의 정의는 아래와 같습니다.
퍼셉트론은 이진 분류를 위한 지도학습 알고리즘 중 하나이다. 이진 분류기는 숫자로 된 벡터를 인풋이 어떤 특정 분류 그룹에 속하는지를 판단할 수 있는 함수이다. 이것은 선형 분류기 중 하나이다. 다시 말하면, 피처 벡터와 가중치의 조합을 통해 선형 예측함수를 기반으로 예측을 만들 수 있는 분류 알고리즘을 말한다.
In machine learning, the perceptron is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class.[1] It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector.
쉽게 풀어서 설명해 드리겠습니다.
퍼셉트론은 아주 간단히 말하면 '알고리즘' 입니다. 조금 더 길게 설명하면 '분류 알고리즘'입니다. 더 길게 설명하면 '여러 데이터 항목의 입력을 받아서 출력은 이진으로 0또는 1을 출력하는 분류 알고리즘' 입니다. 이것은 시그모이드 함수에서와 유사하게 아래와 같은 공식으로 정의 할 수 있습니다.
g(z) = { 1 : z >= 0, 0 : z < 0 }
입력 z가 0 과 같거나 더 크면 1, 0보다 작으면 0을 출력하는 함수 입니다. 이것이 퍼셉트론 알고리즘 입니다. 이것을 그림으로 그려보면 아래 왼쪽과 같습니다. 오른 쪽은 시그모이드 함수의 그림입니다. (시그모이드 함수에서는 지수를 써서 부드러운 곡선으로 표시되었군요.) 그림 아래에는 이러한 함수의 가중치(세타, theta, θ)를 찾기위한 업데이트 방법(Gradient Descent)을 표시합니다.

모델과 비용함수를 정의했으니 데이터를 가지고 어떻게 적용되는지 알아보겠습니다. 1개의 데이터는 여러개의 피처를 가질 수있습니다. (주택 가격예측의 예에서 처럼 주택 크기, 주택 방 수 등 여러개를 가질 수 있습니다. 주택 크기 x1, 주택 방 수 x2)

중앙에 사선으로 가로지르는 점선이 분류 모델의 기준 선입니다. 그래서 오른쪽 위의 사각형과 왼쪽 아래의 원을 분류하는 모델 입니다. 사각형이 1, 원이 0 클래스라고 할때 아래의 그림처럼 새로운 사각형 데이터(x)가 들어오면 모델에서는 잘못 분류하게되고 이를 학습하기 위해 θ를 업데이트하게 됩니다.

아래 그림은 θ를 θ' 으로 업데이트하고 이에 따라 모델 선을 파란색 처럼 변경한 후의 그림 입니다. 이렇게 하니까 사각형 x 가 잘 분류되게 됩니다. 즉 학습이 잘 되었습니다. 이처럼 x 값에 따라서 θ를 업데이트 하게됩니다.
θ ≈ x | y = 1 y가 1일때 세타는 x와 가까워 집니다
θ ≠ x | y = 0 y가 0일때 세타는 x와 멀어 집니다
위와 같이 되는 이유는 x와 θ가 모두 벡터인데 두 벡터의 합이 같은 방향이면 커지고 90도 이상으로 벌어진 경우 작아지기 때문입니다.

이러한 방법으로 훈련 데이터를 이용해서 최적의 θ와 모델선을 찾는 것을 모델 학습 이라고 합니다. 모든 훈련데이터에 대해서 모델 학습이 끝나고 난 뒤 최종의 θ와 모델을 이용해서 예측(Prediction)을 실행할 수 있습니다.
Exponential Family(지수계열, 지수족)
Exponential Faimily는 지수함수와 연관되어 있는 특정 확률분포 종류를 말합니다. 그래서 정규분포에 대한 확률밀도함수, 베르누이분포에 대한 확률밀도함수, 가우시안 분포에 대한 확률밀도함수 등에 대해서 설명합니다. 다양한 분포에 대한 확률밀도함수를 배우는 이유는 y의 분포 유형에 따라서 적절한 추가 함수를 만들어서 모델을 적용해야하기 때문입니다. 뒤에 GLM에서 더 자세히 설명해 드립니다.



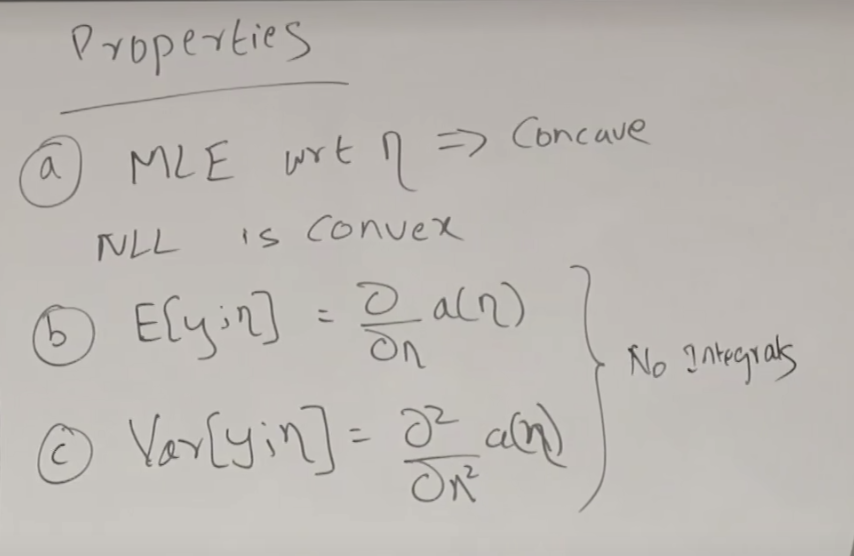
이러한 지수함수 계열은 데이터의 유형에 따라 선택해서 모델에 사용될 수 있습니다. 예를 들면 실수일 경우에는 가우시안을 이진 데이터의 경우 베르누이를, 양수(integer)인 경우 프아송을 , 감마를, 여러차원의 값인 경우 드리크레를 사용할 수 있습니다.

Generalized Linear Model(GLM, 일반화 선형 모델)
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to be a function of its predicted value.(소스 위키피디아)
GLM은 선형회귀의 일반화된 버전이라고 할 수 있습니다. 이것은 선형 모델이 링크 함수를 통해 반환 값에 영향을 주거나 예측된 값에 각 분산에 따른 변량을 적용하는 것에 의해 선형회귀를 일반화 한다. 아래 이미지의 하단에 있는 그림처럼 선형모델을 통해 에타(η) 를 찾아내고 이 에타를 분포에 따른 변형 지수함수가 적용된 모델에 입력으로 사용하여 최종 아웃풋을 산출하는 모델이다.

1) x와 세타가 주어졌을때 y의 값은 지수함수계열에 훈련해서 찾은 에타를 적용한 것과 유사하다
2) 에타는 세타 트렌스포즈와 x를 곱한 것과 같다
3) 테스트할 때 아웃풋은 x와 세타가 주어졌을때 y가 나올 확률이다.
오른쪽 위/아래 2개의 화살표중 위는 training, 아래는 inference할 때의 내용을 말합니다. 여기서 에타(η)는 선형모델의 훈련을 통해 나온 결과 값이라는 것이 중요합니다. 훈련 시 입력된 데이터가 아닙니다.

3개의 파라메타가 필요합니다.

아래는 GML에서 베르누이 분포를 이용한 GML 을 정리한 것인데 결국, 로지스틱 회귀의 경우 즉 시그모이드 함수를 이용한 경우와 같은 표현이 됩니다.

아래는 정규분포를 가정한 일반 선형회귀 모델의 경우 데이터의 분포와 모델 라인을 설명하는 그림입니다. 오른쪽의 점으로 표시된 데이터를 가지고 세타를 찾기위해 비용함수와 GD(경사하강법)를 이용하고 찾은 세타를 이용해서 회귀 선을 그릴 수 있고, 그선이 의미하는 것은 각 x에 해당하는 y 값은 정규분포의 중심에 해당한다고 해석할 수 있습니다.

아래는 분류모델을 설명하는 이미지 입니다. 각 x에 해당하는 확률 값을 정리해보면 모델 라인을 기준으로 시그모이드 그래프와 같은 선이 그려집니다.

Softmax Regression(Multiclass classification)
(1:08:08)
동그라미, 삼각형, 사각형에 대한 분류를 하는 소프트맥스 회귀를 알아보겠습니다.

관련된 기호 셜명을 먼저 합니다.

선형회귀에서 하나의 y값을 만들기 위해 여러 x가 입력되는 경우 여러 개의 세타가 필요하여 θj 로 표시했습니다. 소프트맥스에서는 여러개의 클래스(동그라미, 삼각형, 사각형)가 있으므로 θj도 여러개가 필요하여 행렬로 표시할 수 있습니다. 여기서는 class의 약자를 써서 θc 라고 합니다.

클래스마다 여러 개의 세타가 있습니다.
학습된 θ를 이용해서 각 모델의 분류선을 그려보면 아래와 같습니다.

그럼 이제부터 위 모델을 이용하여 새로운 데이터(사각형에 가까운)가 주어졌을 때 어떤 클래스로 구분할지를 설명합니다. 각 클래스별로 시그모이드 함수의 결과에 해당하는 값들이 나옵니다. 이 값을 지수화하여 모두 양수화 시키면 오른쪽 그래프와 같이 됩니다.

지수화된 것을 다시 정규화(Normalize)하면 좌측의 아래 그래프와 같이 됩니다. 그러나 우리가 최종으로 원하는 것은 오른쪽 아래 그래프 처럼 클래스중에서 하나만 값이 있는 것입니다. 어떤 클래스에 해당하는지를 표시하는 것 입니다.

좌측의 그래프 분포를 오른쪽의 그래프 분포로 바꾸는 것이 가능한데 이것을 Cross Entropy 로 할 수 있습니다. 공식은 아래와 같습니다.

위 공식을 가지고 GD를 이용해서 최적의 각 세타 값을 찾아서 적용하면 변환된 값을 구할 수 있습니다. 크로스 엔트로피의 파라메타를 찾을 때도 경사하강법(GD)를 쓰네요.
아래는 강의 동영상 링크입니다.
https://www.youtube.com/watch?v=iZTeva0WSTQ&list=PLoROMvodv4rMiGQp3WXShtMGgzqpfVfbU&index=4