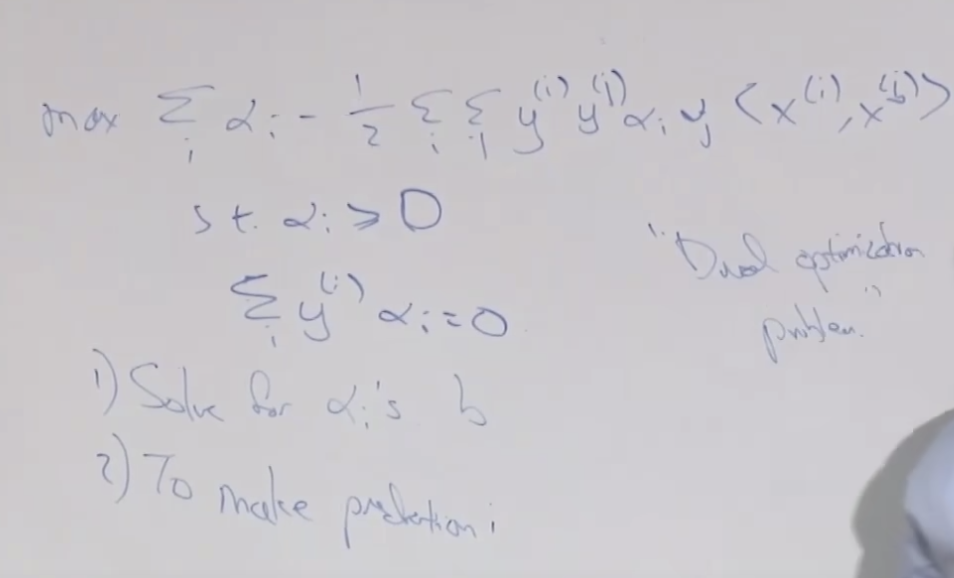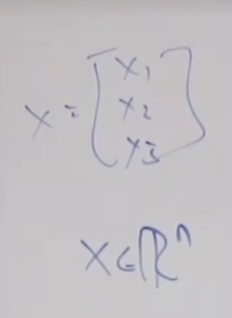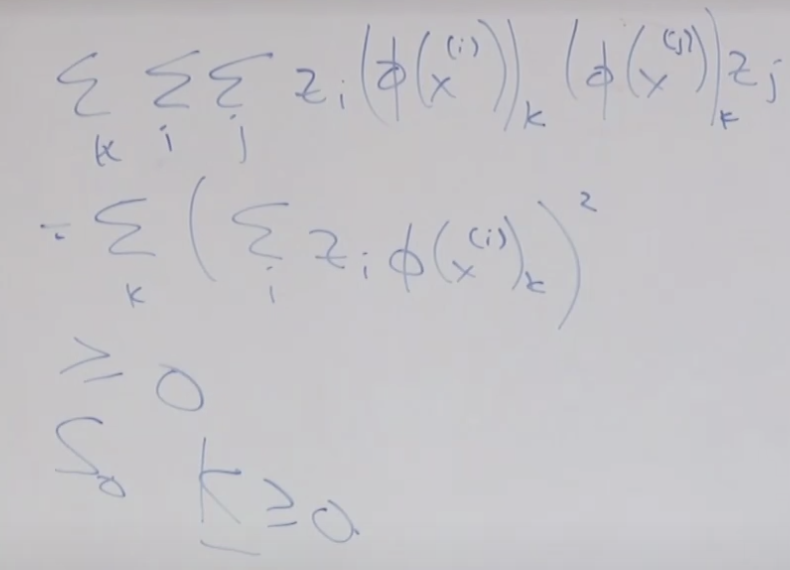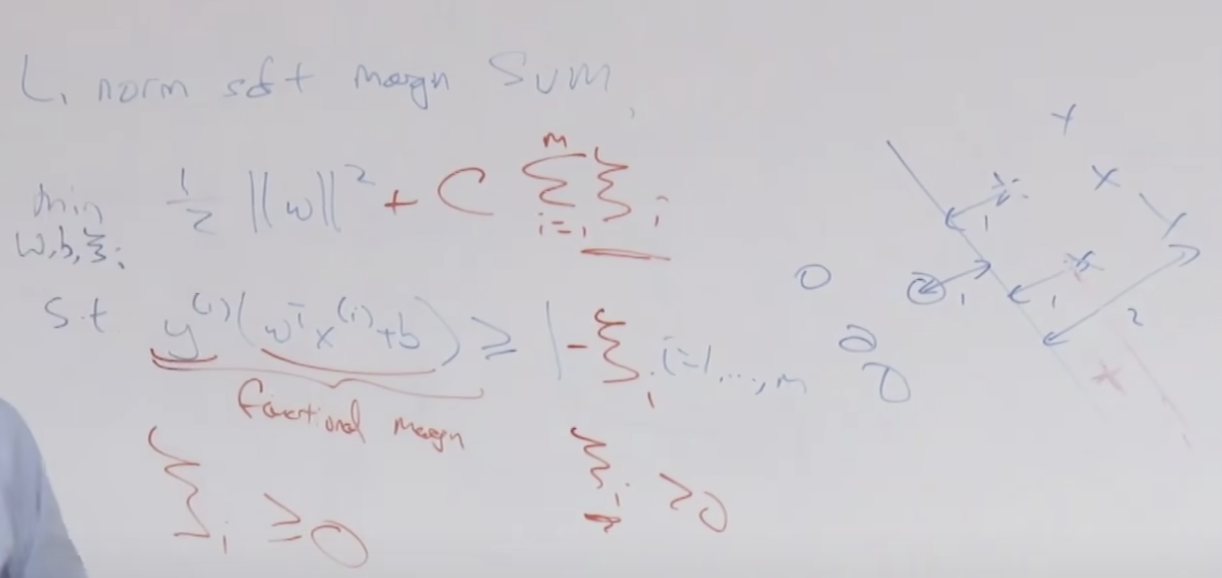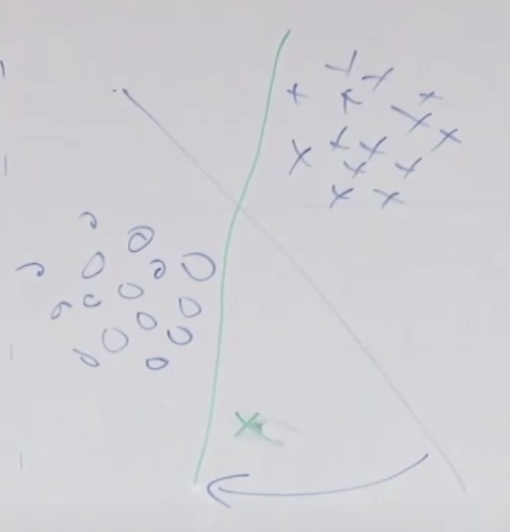Lecture 14 - Expectation-Maximization Algorithms | Stanford CS229: Machine Learning (Autumn 2018)

주요내용

• Unsupervised Learning(비지도 학습)
  • K-means Clustering
  • Mixture of Gaussian: Gaussian Mixture Model (GMM)
  • EM (Expectation-Maximization)
  • Derivation of EM

비지도 학습은 이전까지 배웠던 지도학습과 다른 학습 방법입니다. 예를 들면 지도학습은 긍정 데이터와 부정 데이터들이 주어지고 이들을 잘 분류하는 선형 회귀 모델 같은 것을 만들어서 잘 분류하는 회귀선을 만드는 것이었습니다. 그러나 비지도 학습은 레이블이 없는 데이터들이 주어지고, 지도학습에서는 (x, y)가 주어졌지만 비지도 학습에서는 x 만 제공됩니다. 이런 데이터 셋은 {x(1), x(2), ....x(m)} 으로 주어진 x 데이터 m개를 표현할 수 있습니다. 

K-means Clustering

첫번째로 이야기할 비지도 학습은 클러스터링 입니다.  x 데이터가 주어지면 두개 또는 그 이상의 그룹으로 묶는 알고리즘 입니다. 가장 많이 사용되는 클러스터링은 시장 구분(Market Segmentation)입니다. 예를 들면 사용자들을 클러스터링하여 어떤 다른 시장으로 그룹핑할 수 있는지 알 수 있습니다. 고객의 나이, 성별, 교육, 지역 등을 가지고 클러스터링 하여 다른 그룹으로 만들 수 있습니다. 

위와 같은 데이터 셋이 제공되면 2개의 그룹으로 클러스터링 하기를 원할 것입니다. k-means의 경우 임의로 클러스터 갯수에 해당하는 위치를 선정하고 

데이터 별로 두개의 중심점 중에서 어느 중심점에 더 가까운지를 기준으로 클러스터(색)를 정합니다.

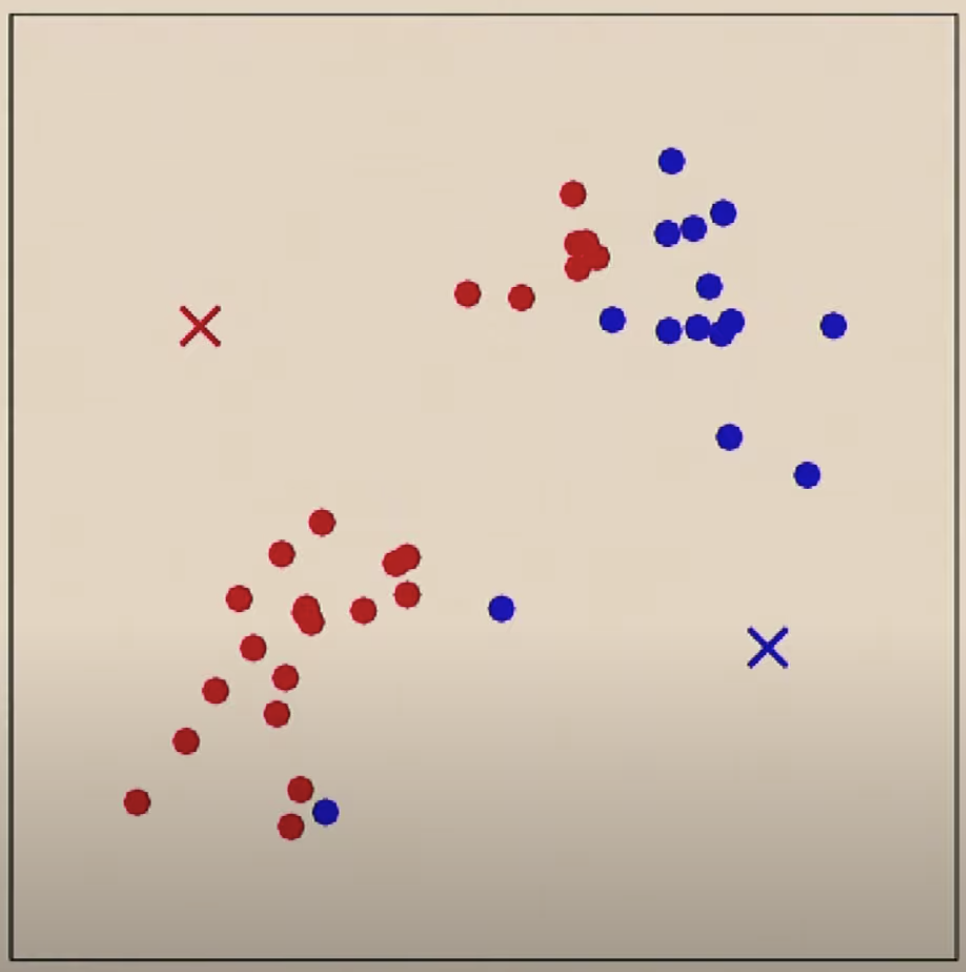
두 번째로는 파란색 점들의 평균을 구해서 새로운 중심점으로 정합니다.  

그리고는 새로 정해진 중심점을 기준으로 모든 점들에 대해서 다시 어느 중심점이 더 가까운지 비교하여 새로운 클러스터를 할당합니다.

그리고 다시 새롭게 할당된 클러스터의 중심점을 구합니다.

 이런 클러스터를 할당하고 새로운 중심점을 구하는 동작을 반복하다 보면 특정 지역에 중심점이 수렴하게 됩니다.

이런 알고리즘을 k-means 알고리즘이라고 합니다.

레이블 되지 않은 Data x 가 주어졌을 때 알고리즘은 아래와 같습니다. 1. 먼저 중심점을 초기화 합니다. k 갯수 만큼의 중심점의 초기 값을 정하는 것인데 보통 random 값으로 잡지 않고 실제 Data x 값들 중에서 k 개를 임으로 선택합니다. 

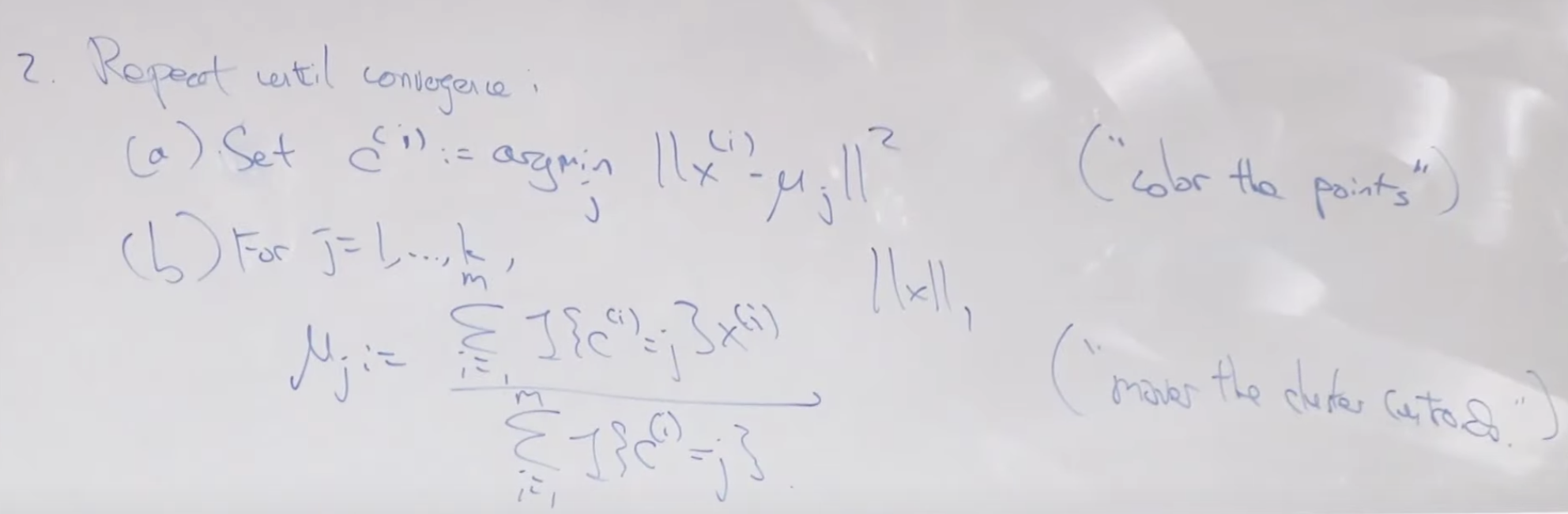
비용함수를 공식으로 적어보면 아래와 같습니다. c는 각 점들을 의미하고, u 뮤는 중심점을 의미 합니다. 각 x 값과 중심점과의 차이를 모두 더한 값으로 반복할 수록 작은 값으로 수렴하게 됩니다. 아주 많은 데이터를 가지고 이 알고리즘을 돌리다보면 아래의 그래프 처럼 수렴하기 전에라도 어느 정도 중심점이 변하지 않으면 종료하기도 합니다.

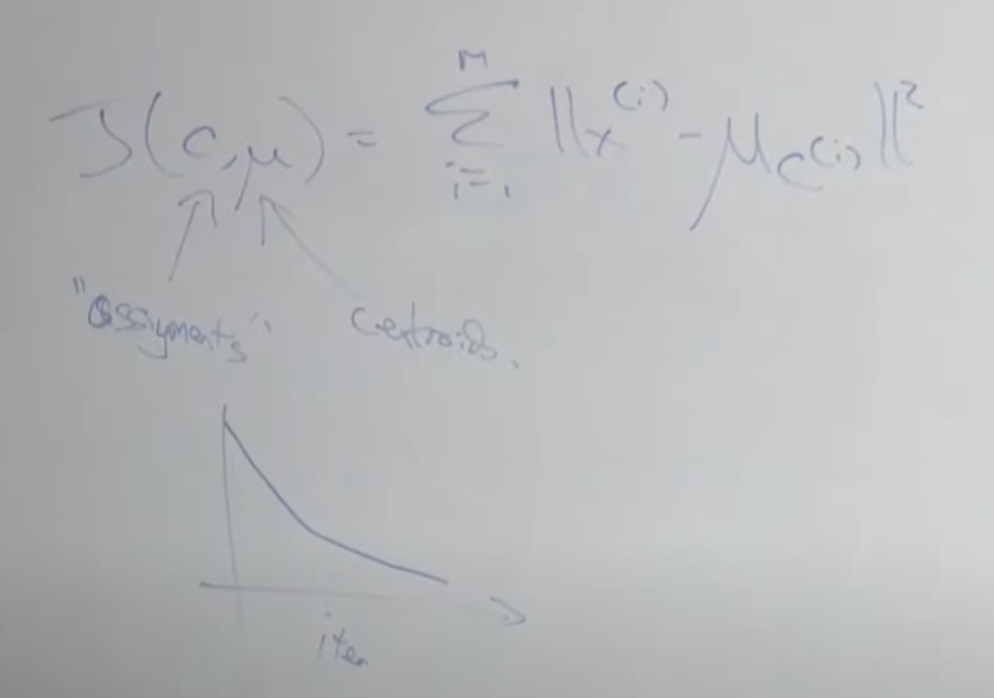
k-means 클러스터링과 관련해서 가장 많이 받는 질문은 어떻게 k 값을 정하는가? 입니다.  메트릭이 있기는 하지만 잘 쓰지는 않습니다. 보는 사람마다 다르게 판단할 수 있기 때문에 모호합니다.

오히려 목적에 맞게 k를 정하는 것을 권합니다. 예를 들어 마케팅을 위해 마켓 세그멘테이션이 필요하고 이를 위해 클러스터링을 한다고 했을때, 그룹핑을 4개로 할 수도 있고 100개로 도 할 수 있지만 업무적으로 프로모션을 위한 그룹 설계가 4개로 준비되어 있을 경우 4개로 그룹핑하여 제공해야 실무에서 마케팅에 사용할 수 있습니다.

k-means 알고리즘은 로컬 미니멈에 빠질 수 있습니다. 이 말은 초기 중심점 값을 어떻게 정하냐에 따라서 알고리즘을 실행할 때마다 다르게 그룹핑 될 수 있다는 의미입니다. 이런 로컬 미니멈에 빠지는 것을 방지하는 방법중 하나는 여러번 알고리즘을 실행 시키고 나서 비용함수의 값이 제일 작은 결과로 정해진 클러스터 결정을 선택하는 것입니다.

Density estimation

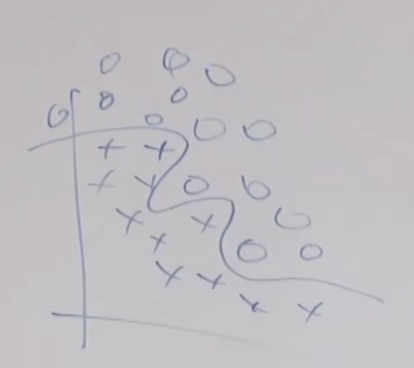
비행기 엔진을 만드는 공장에서 만들어진 엔진의 불량을 탐지하는 모델을 만든다고 생각해 보시죠. 시험 테스트 중에 나온 데이터인 진동 Vibration과 발열 Heat을 가지고 그래프를 만들었을 때 아래와 같이 그려진다고 하겠습니다. 이 때 녹색 점과 같은 데이터를 만들어낸 비행기 엔진의 경우 이상 탐지(Anomaly Detection)으로 탐지 할 수 있습니다.

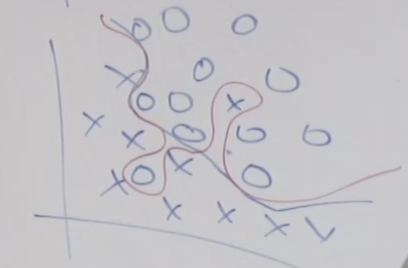
그러나 아래와 같이 분포가 간단하지 않은 경우 그룹핑을 하기 매우 어렵습니다. 이럴때 아래쪽에 있는 두개의 타원형 형태의 가우시안 분포와 이 타원형의 왼쪽에 연결된 또 다른 두개의 타원형 형태의 가우시안 분포, 즉 2개의 가우시안 분포로 전체 분포를 설명할 수 있습니다.

1차원 가우시안 분포를 예를 들어 보겠습니다. 아래와 같이 X 데이터가 주어졌을 때 이것은 2개의 가우시안 분포에서 왔을 수 있습니다. 그리고 이번 예시의 경우 두 개의 분포를 연결하면 중앙 부분은 확률이 낮아지는 부분으로 구성된 하나의 분포 곡선을 그릴 수 있습니다. (아래쪽 쌍봉 곡선)

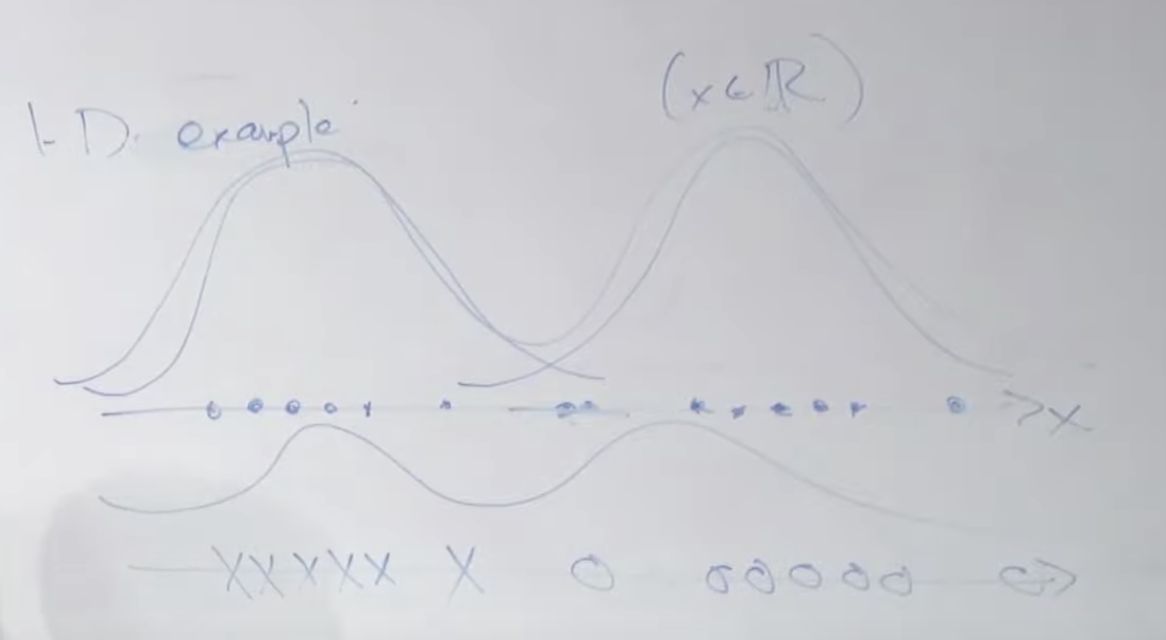
Mixture of Gaussians Model: Gaussian Mixture Model (GMM)

이러한 방법으로 여러개의 다변량 분포가 혼합되어 있는 경우 어느 분포에서 추출될 가능성이 높은지를 알 수 있습니다.

latent 는 hidden 또는 unobserved의 의미 입니다. z는 랜덤 변수값이고 다중 분포일때 z ㅌ {1, ... k} , x(i), z(i)는 결합 분포를 가지고 있습니다. 이 것은 P(x(i), z(i)) = P(x(i) | z(i)) P(z(i)) 로 계산됩니다. 

일반적으로 GDA Gaussian Distribution Analysis 는 2개의 분포, 즉 베르누이 분포를 말하지만 여기에서는 k개의 분포를 가지는 다형성의 파이를 갖습니다. 이 것이 첫번째로 GDA와 다른 것이고 두번째는 j분포 갯수의 차이 입니다. z(i)가 j번째 가우시안 분포에서 나왔을때 x(i)가 나올 확률은 평균이 uj 이고 분산이 시그마j 인 정규분포에서 나올 확률과 같습니다.  GDA와 가장 큰 차이점은 GDA는 데이터 y(i)가 관측된 값으로 주어진다는 것입니다. 

만약 우리가 z(i)의 값들을 알고 있다면 MLE를 사용할 수 있습니다. 그때 가능도는 아래와 같이 구할 수 있습니다.

EM (Expectation-Maximization)

EM은 관측되지 않는 잠재변수에 의존하는 확률 모델에서 최대가능도(maximum likelihood)나 최대사후확률(maximum a posteriori, 약자 MAP)을 갖는 모수의 추정값을 찾는 반복적인 알고리즘을 말합니다. (위키피디아)

첫번째 E-step은 아래와 같습니다. 우리는 실제 z(i) 값을 모르기 때문에 주어진 값들을 이용해서 기대값을 찾는 단계입니다. 여기서 z(i)란 x(i)가 뽑힐 수 있는 특정 정규분포 j를 말합니다.

두번째 단계는 M-step 입니다. 앞에서 찾은 기대값을 최대로하는 모수 값을 찾습니다.

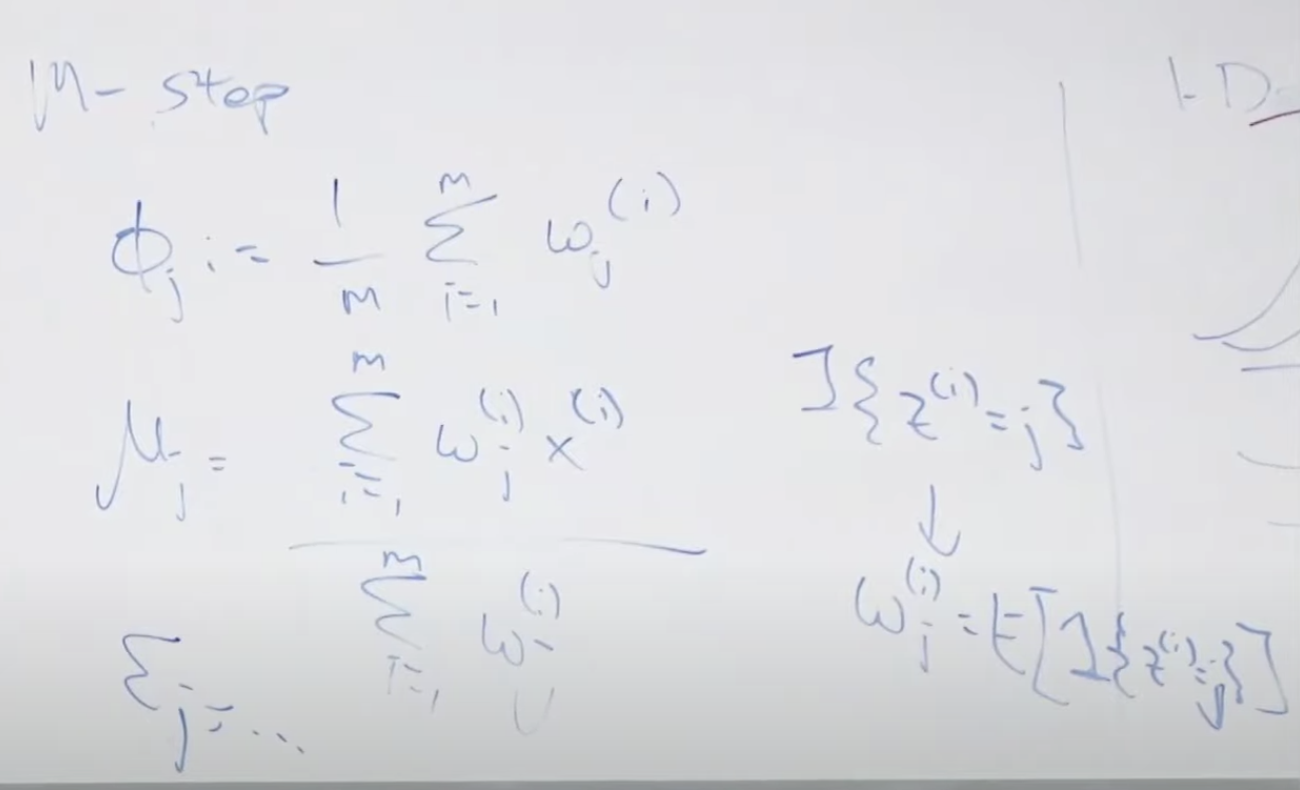
이러한 단계를 거처 기대값을 최대로 하는, 여러개의 분포가 합쳐지는 하나의 분포 곡선을 만들 수 있습니다. 이러한 곡선은 아래처럼 다양합니다.  이로써 찾은 함수를 통해 입력값 x를  실행했을때 결과 확률값이 특정 기준(입실론) 보다 크거나 같으면 정상적인 데이터이고 확률값이 작으면 이상탐지(Anomaly)로 판단할 수 있습니다.

Derivation of EM

이후 아래는 EM의 공식을 유도하는 내용입니다.

Jensen's inequality

함수 f를 아래로 볼록한 함수(Convex function)이라고 하고 x를 임의의 값이라고 할때, 공식 f(EX) <= E[f(x)] 를 만족합니다.

우리는 젠슨의 불균형 공식을 위로 볼록한 Concave 함수로 사용합니다. Concave 함수는 Convex 함수와 위/아래가 바뀐 함수이지요. 그럴 경우 위에서 설명한 모든 부등식을 반대로 바꾸면 됩니다.

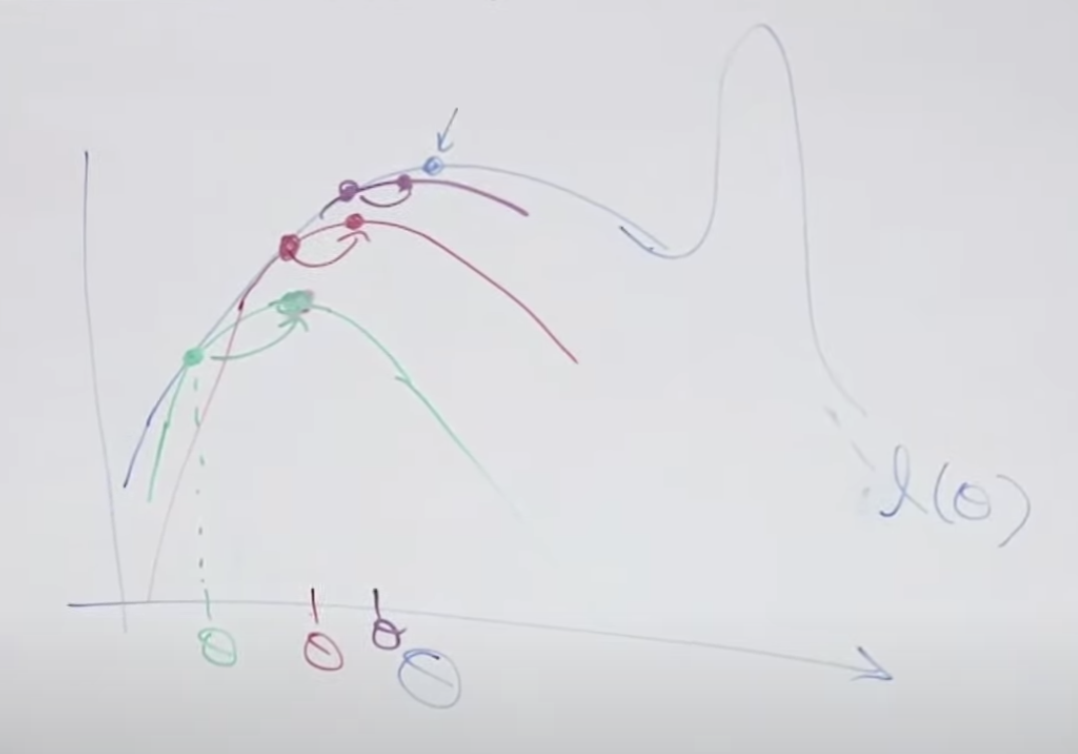
임의의 녹색 theta세타 값을 먼저 설정합니다. 이 값에 해당하는 함수곡선(녹색)을 만들고 이 함수와 목표 함수(검정색)가 만나는 점을 찾고 이 녹색 함수의 꼭지점을 찾습니다. 그리고 이 꼭지점으로 이동합니다. 이 꼭지점에 해당하는 theta값으로 변경 후 다시 함수를 찾습니다. 이러한 내용을 반복하면 검정색의 목표 함수의 지역 최대값(꼭지점)에 점점 가깝게 됩니다. 그러나 아래 그림의 오른쪽 처럼 목표함수가 여러개의 지역 최대값을 가지고 있는 경우 전체 최대값을 찾지 못할 수도 있습니다.

아래는 이러한 E, M 단계를 공식으로 풀이 증명하는 내용입니다.

위 공식의 변형에 필요한 기본 전제 공식은 아래와 같습니다.

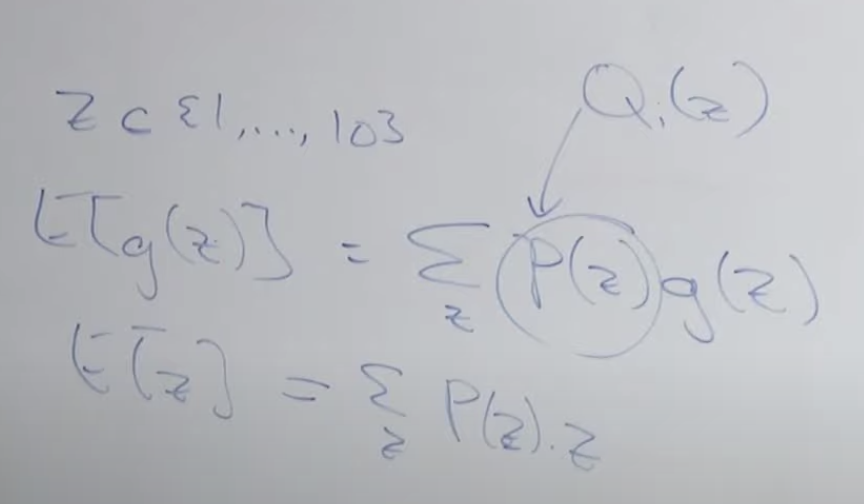
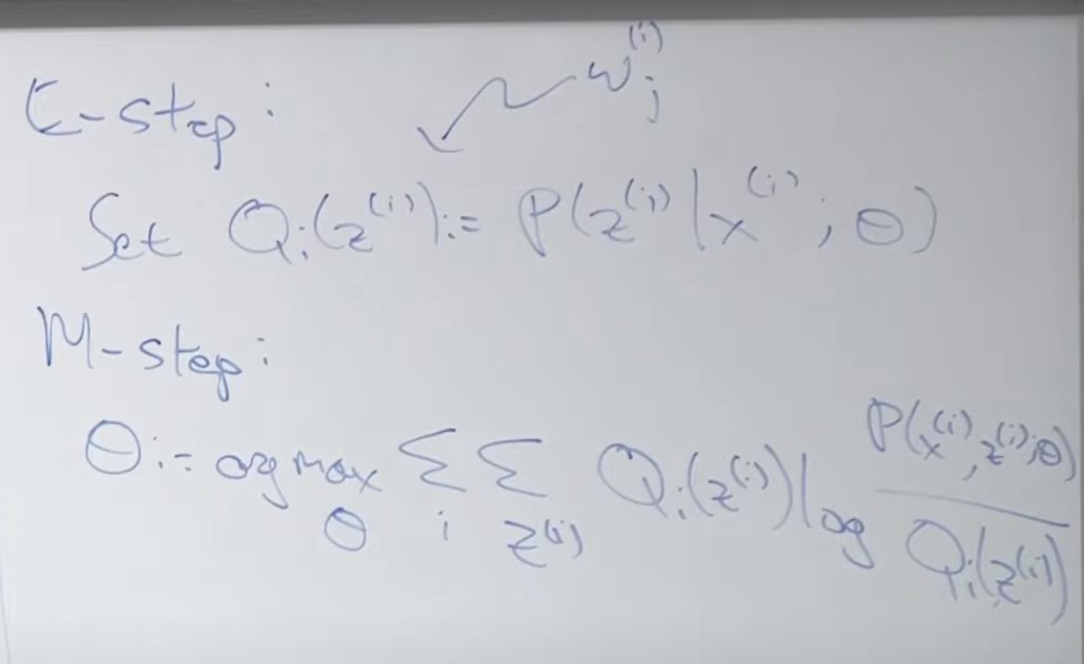
아래는 강의 동영상 링크 입니다.

https://www.youtube.com/watch?v=rVfZHWTwXSA&list=PLoROMvodv4rMiGQp3WXShtMGgzqpfVfbU&index=14 

스탠포드 머신러닝 강의 1:20 / 1:20:24Lecture 7 - Kernels | Stanford CS229: Machine Learning (Autumn 2018)

주요내용

• Optimization Problem
• Representer Theorem
• Kernels (SVM)
• Examples of Kernels (SVM)

Recap

지난 시간에 배웠던 내용을 정리합니다. Optimal margin classifier를 설명합니다.

감마를 최대화하는 w와 b를 구하면 됩니다. 이말은 모든 예제가 구해지면 감마보다 큰 지오매트릭 마진을 같는다는 의미 입니다. 모든 셈플을 잘 분리한다는 말이지요. (반대로 이말은 아웃라이어가 있을때 민감하게 반응한다는 단점이 있습니다. 이것을 어떻게 해결하는지는 뒤에서 설명합니다.)

w와 b에 일정한 값을 곱해도 같은 직선이라는 것을 설명합니다.

Gradient Descent 를 설명합니다.

w는 경계선의 기울어짐을 결정하고 b는 경계선의 수직방향으로의 이동 정도를 결정합니다.

이 내용을 3차원에서 설명해보면 아래와 같습니다. 3차원에서는 2차원에서의 선이 평면으로 나타납니다. 아래 예시에서 w는 평면의 각도를 결정합니다. w3이 0 이라서 수직이 되었네요.

w를 구하기 위한 상세 공식 유도를 아래와 같이 설명합니다.

24:34

Kernel Trick 커널 트릭

커널 트릭은 아래와 같습니다.
1) 커널은 이너프러덕으로 계산된다
2) 피처 x가 2개든, 3개든 얼마든지 매핑 함수를 통해 100,000 또는 수억개의 피처로 만들 수 있다. (아래 그림의 오른쪽 내용)
3) 2)에서 매핑된 변수(Φ(x))들과 z 함수(Φ(z))들을 계산하는 방법을 찾는다.
4) 알고리즘에 있는 <x, z> 를 k<x, z> 로 바꾼다.
이말을 합처보면 고차원 매핑(2)과 내적(3)을 하는 것이 커널 입니다.

커널의 예를 들어 보겠습니다.
x 는 아래와 같습니다.

그러면 아래와 같이 x를 고차원으로 매핑시킨 Φ(x)와 여러변수의 Φ(z)를 만들 수 있습니다. : 여기에서 매핑함수 Φ() 는 R^(n^2)로 정의했기 때문에 3개의 변수(x1, x2, x3)가 9개의 변수(x1,x1, x1,x2, ...)로 변경되었습니다. 이를 계산하기 위해서는 O(n^2)의 시간이 필요합니다.

더 좋은 방법을 생각해 보겠습니다. 아래 그림의 제일 위에 있는 공식 처럼 k(x,z) 를 다른 계산 방법으로 바꿀 수 있습니다. 즉, 함수를 거치지 않고 두 행렬의 곱으로 계산할 수 있습니다. 아래는 (x^Tz)^2가 Φ(x)^T Φ(z)와 같음을 증명하는 내용입니다. (x^Tz)^2 를 두개로 나누어서 () () 이렇게 만들었고 아래 처럼 쭉 따라서 가다보니 결국 (빨간색/녹색 동그라미처럼 두 항목을 곱한 값을 더한다는 것과 같은데...이말은 결국 제일 위줄 공식의 가운데에 있는 Φ(x)^T Φ(z)와 같은 결과이기 때문에 두 공식이 같음이 증명됩니다.
속도는 둘다 R^n 행렬이기 때문에 T 트렌스포즈하고 곱을 하면 O(n) 시간만 있으면 계산이 됩니다.

다시말하면 결국 Φ(x)의 한 행의 내용(빨간 동그라미)과 Φ(z)의 한 행의 내용(녹색 동그라미)을 곱해서 합친 것이 (x^Tz)^2와 같습니다.

여기에 상수 c를 추가해도 역시 소요시간은 O(n) 입니다. Φ(x)는 n+d 중에 d개의 피처를 갖을 수 있는데 최대 d의 깊이를 가질 수 있습니다. 그래서 d=5라면 아래와 같이 x1, x2, x3, x12, x29 도 될수 있고 x1, x2^2, x2,x18 도 될 수 있습니다. 이것은 (n+d)^d 와 비슷합니다.

SVM을 정의 하면
Optimal margin classifier + Kernel Trick = Support Vector Machine
이 됩니다.
이말은 적은 데이터로 많은 피처들을 만들어서 아주 효율적으로 계산해서 효과적으로 분류하는 모델을 만들게 됨을 의미합니다. SVM이 다른 말로 커널인줄 알았는데 조금 다른 것이 이었네요.
아래의 영상을 통해 SVM이 어떻게 동작하는 지 이해를 높일 수 있습니다.
https://www.youtube.com/watch?v=3liCbRZPrZA

여러 차원에 있던 데이터들을 잘 분리하는 하이퍼플레인(평면)이 있는데 이런 그래프를 2차원 으로 축소하면 하이퍼블레인(평면)이 선으로 바뀌어 표시됩니다. 그대신 직선이 아닌 구불구불한 선이 될 수 있습니다. 이러한 2차원 결과를 보여주는 것이 아래 그림 입니다. 이해되시나요. 위의 동영상을 보셨다면 이해가 되실 것 같습니다.

자, 이제 커널을 만드는 방법에 대해서 이야기 합니다. 여러 가정/조건이 있습니다. x, z가 비슷하면 커널함수 k(x,z)의 결과가 커야하고, 반대로 다르면 함수의 결과가 작아야 합니다. 이것은 벡터의 성질과 동일합니다. 이러한 조건을 만족하는 함수중하나가 아래의 공식입니다.

또다른 조건은 지금까지 맞다고 가정했던 공식인 k(x,z) = Φ(x)^T Φ(z) 입니다. 그리고 k(x,x) = Φ(x)^T Φ(x) >= 0 입니다. x1 부터 xd까지의 값을 가진 d 포인트가 있다고 합니다. 이때 K(커널행렬)은 R^(d*d) 입니다. 요소의 표시는 K(sub ij) = k(x(i), x(j)) 로 표시합니다.

그래서 벡터 z가 주어졌을때 커널과 계산 공식을 유도해보면 결국 K가 0보다 크거나 같습니다.

이것은 머서이론 (Mercer Theorem)과 같습니다.

그래서 앞서 커널을 만드는 방법을 설명할때 조건과 이에 적합한 예시를 들었던 아래의 커널함수는 유효함을 알수 있고 이것은 가장 많이 쓰이는 가우시안 커널입니다.

그 밖에도 선형 커널이 있는데 이는 선형함수와 같은 결과를 나타냅니다.

커널 트릭 중 이너프러덕은 다른 모델에서도 많이 쓰이는 방법입니다. < x(i), x(j) >


아래와 같이 2차원에 그래프를 그렸을때 빨간색과 같이 모든 것을 잘 분리하는 모델을 만들고 싶지 않을 것입니다. 왜냐하면 실제 추론 시에는 이렇게 할경우 더 안좋은 성능을 내기 때문입니다. 즉, 훈련데이터에 오버피팅 되어서 실제 추론시에는 성능이 낮아지는 것입니다. Variance가 커지겠네요. 그래서 빨간색 분리선보다는, 이상한 자리에 있는 값들은 잘 못 분리하더라도 파란색 분리선처럼 만들고 싶을 것입니다.

이렇게 하기 위해서 정규화를 할 수 있습니다. L1 놈/노름 소프트 마진 SVM 입니다. 오차 c를 이용하여 분리선과 오차거리를 고려해서 분리하게 됩니다.

L1 놈/노름 소프트 마진 SVM을 쓰는 다른 이유는 아웃라이어 하나만 들어와도 많이 다른 분리선을 만들기 때문에 이를 방지하기 위해 L1 norm soft margin SVM을 쓰는 것이 좋습니다. 옵티마이저가 최악의 케이스도 분리/포함하도록 되었는 경우 이와 같은 문제가 있습니다. 녹색 x 하나 만으로 기존에 파란색 선에서 녹색선처럼 많은 각도가 변경됩니다.

가우시안 커널의 성능도 매우 좋은데 MNIST와 같은 이미지 데이터에 대한 분류에서도 높은 성능을 냅니다. 0과 1의 픽셀 정보를 이용해서 하나의 벡터로 만들어서 SVM의 입력으로 넣고 분류하면 됩니다. SVM은 때로는 딥러닝 보다 좋은 성능을 낼때도 있으며 턴키 알고리즘으로 쉽게 만들 수 있습니다.

Examples of Kernels (SVM)

프로틴 시퀀스 분리 모델의 예시입니다. A부터 Z로 표시되는 원소로 구성된 프로틴의 아미노산 유무를 가지고 프로틴의 기능을 분리하는 모델을 만든다고 가정 합니다. 실제로는 20개인데 알파벳을 이용해서 이해를 쉽게하기 위해 26개를 이용합니다. 왼쪽에 시퀀스에서 등장한 4개의 문자를 오른쪽 피처 4개의 문자와 같으면 그 갯수를 누적하여 표시합니다. BAJT는 왼쪽에서 두번 나와서 오른쪽에 2로 표시됬습니다. 이렇게 해서 Φ(x)를 만들고 k(x,x)를 가우시안 커널을 이용하여 만들어 적용하면 됩니다.

SUMMARY

정리하면 SVM은 커널트릭과 최적의 마진 분리를 이용하는 분류 알고리즘 입니다. 커널 트릭은 입력 데이터를 다차원 데이터로 매핑/변환 하는 함수 Φ(x)와 그 결과와 커널함수 k(x,z) 결과의 행렬을 가지고 분류 모델을 만듭니다. 이러한 결과에 정규화 L1 norm soft margin SVM을 이용하고 오차 c를 추가하여 아웃라이어에 강한 분류 모델을 만듭니다. 최적의 마진 분리는 Geometric margin 지오메트릭 마진은 경계선을 근접한 요소와의 거리를 기준으로 경계선을 나누눈 방법입니다. SVM은 턴키 알고리즘으로 쉽게 개발/활용할 수 있을 뿐만 아니라 초기 딥러닝 모델 만큼이나 성능이 좋아서 지금도 많이 쓰입니다.



아래는 강의 영상 링크 입니다.
https://www.youtube.com/watch?v=8NYoQiRANpg&list=PLoROMvodv4rMiGQp3WXShtMGgzqpfVfbU&index=7

스텐포드 기계학습 강의  Lecture 4 - Perceptron & Generalized Linear Model | Stanford CS229: Machine Learning (Autumn 2018)

이번 강의 주요 내용

• Perceptron(퍼셉트론)
• Exponential Family(지수계열, 지수족)
• Generalized Linear Model(GLM, 일반화 선형 모델)
• Softmax Regression(Multiclass classification)소프트맥스 회귀

Perceptron

퍼셉트론을 배우는 이유는 지난 시간에 이어 분류 문제를 다루는 알고리즘 중에서 기본적이고 역사적으로 의미가 있는 알고리즘이기 때문입니다. 너무 간단하고 한계가 많아서 실제로 많이 사용되지는 않지만 이것이 기반이되어 최근에 많이 쓰이는 딥러닝이 발전되었기 때문에 퍼셉트론을 이해하는 것은 중요하다고 할 수 있습니다.

퍼셉트론에 대한 정의와 배경에 대한 이야기가 강의에서는 부족해서 이해하기 어려울 수 있습니다.

그래서 설명을 추가해 보았습니다.

위키의 정의는 아래와 같습니다.

퍼셉트론은 이진 분류를 위한 지도학습 알고리즘 중 하나이다. 이진 분류기는 숫자로 된 벡터를 인풋이 어떤 특정 분류 그룹에 속하는지를 판단할 수 있는 함수이다. 이것은 선형 분류기 중 하나이다. 다시 말하면, 피처 벡터와 가중치의 조합을 통해 선형 예측함수를 기반으로 예측을 만들 수 있는 분류 알고리즘을 말한다. 

In machine learning, the perceptron is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class.[1] It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector.

쉽게 풀어서 설명해 드리겠습니다.

퍼셉트론은 아주 간단히 말하면 '알고리즘' 입니다. 조금 더 길게 설명하면 '분류 알고리즘'입니다. 더 길게 설명하면 '여러 데이터 항목의 입력을 받아서 출력은 이진으로 0또는 1을 출력하는 분류 알고리즘' 입니다.  이것은 시그모이드 함수에서와 유사하게 아래와 같은 공식으로 정의 할 수 있습니다. 

g(z) = { 1 : z >= 0,      0 : z < 0 }

입력 z가 0 과 같거나 더 크면 1, 0보다 작으면 0을 출력하는 함수 입니다. 이것이 퍼셉트론 알고리즘 입니다. 이것을 그림으로 그려보면 아래 왼쪽과 같습니다. 오른 쪽은 시그모이드 함수의 그림입니다. (시그모이드 함수에서는 지수를 써서 부드러운 곡선으로 표시되었군요.) 그림 아래에는 이러한 함수의 가중치(세타, theta, θ)를 찾기위한 업데이트 방법(Gradient Descent)을 표시합니다.

모델과 비용함수를 정의했으니 데이터를 가지고 어떻게 적용되는지 알아보겠습니다. 1개의 데이터는 여러개의 피처를 가질 수있습니다. (주택 가격예측의 예에서 처럼 주택 크기, 주택 방 수 등 여러개를 가질 수 있습니다. 주택 크기 x1, 주택 방 수 x2)

중앙에 사선으로 가로지르는 점선이 분류 모델의 기준 선입니다. 그래서 오른쪽 위의 사각형과 왼쪽 아래의 원을 분류하는 모델 입니다. 사각형이 1, 원이 0 클래스라고 할때 아래의 그림처럼 새로운 사각형 데이터(x)가 들어오면 모델에서는 잘못 분류하게되고 이를 학습하기 위해 θ를 업데이트하게 됩니다.

아래 그림은 θ를 θ' 으로 업데이트하고 이에 따라 모델 선을 파란색 처럼 변경한 후의 그림 입니다. 이렇게 하니까 사각형 x 가 잘 분류되게 됩니다. 즉 학습이 잘 되었습니다. 이처럼 x 값에 따라서 θ를 업데이트 하게됩니다.

θ  ≈  x | y = 1    y가 1일때 세타는 x와 가까워 집니다

θ  ≠  x | y = 0    y가 0일때 세타는 x와 멀어 집니다

위와 같이 되는 이유는 x와 θ가 모두 벡터인데 두 벡터의 합이 같은 방향이면 커지고 90도 이상으로 벌어진 경우 작아지기 때문입니다.

이러한 방법으로 훈련 데이터를 이용해서 최적의 θ와 모델선을 찾는 것을 모델 학습 이라고 합니다. 모든 훈련데이터에 대해서 모델 학습이 끝나고 난 뒤 최종의 θ와 모델을 이용해서 예측(Prediction)을 실행할 수 있습니다.

Exponential Family(지수계열, 지수족)

Exponential Faimily는  지수함수와 연관되어 있는 특정 확률분포 종류를 말합니다.  그래서 정규분포에 대한 확률밀도함수, 베르누이분포에 대한 확률밀도함수, 가우시안 분포에 대한 확률밀도함수 등에 대해서 설명합니다.  다양한 분포에 대한 확률밀도함수를 배우는 이유는 y의 분포 유형에 따라서 적절한 추가 함수를 만들어서 모델을 적용해야하기 때문입니다. 뒤에 GLM에서 더 자세히 설명해 드립니다.

이러한 지수함수 계열은 데이터의 유형에 따라 선택해서 모델에 사용될 수 있습니다. 예를 들면 실수일 경우에는 가우시안을  이진 데이터의 경우 베르누이를, 양수(integer)인 경우 프아송을 ,  감마를, 여러차원의 값인 경우 드리크레를 사용할 수 있습니다.

Generalized Linear Model(GLM, 일반화 선형 모델)

In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to be a function of its predicted value.(소스 위키피디아)

GLM은 선형회귀의 일반화된 버전이라고 할 수 있습니다. 이것은 선형 모델이 링크 함수를 통해 반환 값에 영향을 주거나 예측된 값에 각 분산에 따른 변량을 적용하는 것에 의해 선형회귀를 일반화 한다. 아래 이미지의 하단에 있는 그림처럼 선형모델을 통해 에타(η) 를 찾아내고 이 에타를 분포에 따른 변형 지수함수가 적용된 모델에 입력으로 사용하여 최종 아웃풋을 산출하는 모델이다.

1) x와 세타가 주어졌을때 y의 값은 지수함수계열에 훈련해서 찾은 에타를 적용한 것과 유사하다

2) 에타는 세타 트렌스포즈와 x를 곱한 것과 같다

3) 테스트할 때 아웃풋은 x와 세타가 주어졌을때 y가 나올 확률이다.

오른쪽 위/아래 2개의 화살표중 위는 training, 아래는 inference할 때의 내용을 말합니다. 여기서 에타(η)는 선형모델의 훈련을 통해 나온 결과 값이라는 것이 중요합니다. 훈련 시 입력된 데이터가 아닙니다. 

3개의 파라메타가 필요합니다.

아래는 GML에서 베르누이 분포를 이용한 GML 을 정리한 것인데 결국, 로지스틱 회귀의 경우 즉 시그모이드 함수를 이용한 경우와 같은 표현이 됩니다. 

아래는 정규분포를 가정한 일반 선형회귀 모델의 경우 데이터의 분포와 모델 라인을 설명하는 그림입니다.  오른쪽의 점으로 표시된 데이터를 가지고 세타를 찾기위해 비용함수와 GD(경사하강법)를 이용하고 찾은 세타를 이용해서 회귀 선을 그릴 수 있고, 그선이 의미하는 것은 각 x에 해당하는 y 값은 정규분포의 중심에 해당한다고 해석할 수 있습니다.

아래는 분류모델을 설명하는 이미지 입니다. 각 x에 해당하는 확률 값을 정리해보면 모델 라인을 기준으로 시그모이드 그래프와 같은 선이 그려집니다.

Softmax Regression(Multiclass classification)

(1:08:08)

동그라미, 삼각형, 사각형에 대한 분류를 하는 소프트맥스 회귀를 알아보겠습니다.

관련된 기호 셜명을 먼저 합니다.

선형회귀에서 하나의 y값을 만들기 위해 여러 x가 입력되는 경우 여러 개의 세타가 필요하여 θj 로 표시했습니다. 소프트맥스에서는 여러개의 클래스(동그라미, 삼각형, 사각형)가 있으므로 θj도 여러개가 필요하여 행렬로 표시할 수 있습니다. 여기서는 class의 약자를 써서 θc 라고 합니다.

클래스마다 여러 개의 세타가 있습니다.

학습된 θ를 이용해서 각 모델의 분류선을 그려보면 아래와 같습니다.

그럼 이제부터 위 모델을 이용하여 새로운 데이터(사각형에 가까운)가 주어졌을 때 어떤 클래스로 구분할지를 설명합니다. 각 클래스별로 시그모이드 함수의 결과에 해당하는 값들이 나옵니다. 이 값을 지수화하여 모두 양수화 시키면 오른쪽 그래프와 같이 됩니다.

지수화된 것을 다시 정규화(Normalize)하면 좌측의 아래 그래프와 같이 됩니다. 그러나 우리가 최종으로 원하는 것은 오른쪽 아래 그래프 처럼 클래스중에서 하나만 값이 있는 것입니다. 어떤 클래스에 해당하는지를 표시하는 것 입니다. 

좌측의 그래프 분포를 오른쪽의 그래프 분포로 바꾸는 것이 가능한데 이것을 Cross Entropy 로 할 수 있습니다. 공식은 아래와 같습니다.

위 공식을 가지고 GD를 이용해서 최적의 각 세타 값을 찾아서 적용하면 변환된 값을 구할 수 있습니다.  크로스 엔트로피의 파라메타를 찾을 때도 경사하강법(GD)를 쓰네요.

아래는 강의 동영상 링크입니다.

https://www.youtube.com/watch?v=iZTeva0WSTQ&list=PLoROMvodv4rMiGQp3WXShtMGgzqpfVfbU&index=4 

주요내용:

• Linear Regression(선형회귀)
• Batch/Stochastic Gradient Descent(SGD: 일괄/확률통계 경사 강하법)
• Normal Equation(정규 방정식)

지난 시간에 이야기했던 주택 사이즈를 통한 주택 가격 예측하는 예를 설명합니다.

전통적인 지도학습의 프로세스를 위와 같이 말하면서 결국 기계학습의 목표는 (Inferencing Data)입력을 받았을 때 적절한 추정(Predicted Data의) 예측/매핑 값을 만드는 모델을 만드는 것이라 말합니다.

기계학습 모델을 만들때 상기 프로세스에 있는 요소들에 대한 많은 의사결정들이 필요한데(어떤 데이터를 쓸것인지, 어떤 알고리즘을 쓸것인지 등) 각각에 대해 적합한 의사결정을 하는 것이 좋은 모델을 만드는데 매우 중요하다고 합니다.

선형회귀(Linear Regression)

모델(가설, h)의 표현 방법중하나가 선형회귀(Linear Regression)입니다. 기본표현식은 아래와 같습니다. 입력 데이터 항목이 한 개(x, 예시에서는 주택 크기)가 있는 경우입니다.

h(x)= θ0+ θ1*x

즉, 주택 크기를 입력해서 가격을 예측하는 모델을 만든다고 할경우 x는 주택 크기가 되고 h(x)는 주택 가격(모델의 아웃풋/예측값)이 됩니다.

주택 크기, 방의 수 처럼 항목이 2개인 경우는 h(x)= θ0 * x0 + θ1 * x1 + θ2 * x2  입니다. 

항목이 많아질 경우 수식이 길고 복잡해지므로 간단한 수식으로 정리하면 아래와 같습니다.

향후 나올 표기법들에 대핸 정리해 봅니다.

• θ = parameters 파라메타라고 합니다. feature 수 만큼의 파라메타가 필요하므로 j 개의 백터로 표시할 수 있습니다.
• m = 훈련 데이터 예시의 갯수
• x : "inputs"/features
• y : "outputs"/target
• (x, y) = 하나의 훈련 데이터 예시
• (x(i), y(i)) = i번째 훈련 데이터 예시, x(1) = x의 1번째 훈련 데이터 값
• n = feature 갯수

• 0위에 화살표 = 모든 원소값이 0인 백터
• :=  는 := 오른쪽에 있는 값을 왼쪽으로 할당한다는 표현( a := a + 1의 의미는 a의 값을 1 증가시킴)

좋은 모델은 무엇일까요!  모델의 아웃풋(예측값, h(x))이 실제 정확한 주택 가격인 y와 일치하는 것입니다.  이렇게 잘 일치시키기 위해 모델에서 바꿀 수 있는 값은 파라메터(θ)값 밖에 없습니다. 따라서 적절한/좋은 파라메터를 찾는 것이 좋은 모델을 만드는 것입니다. 다시 말하면 모델의 아웃풋과 실제 y 값의 차이를 작게 만드는 것이 목표입니다. 이것을 공식으로 바꾸어보면 

minimize (h(x^1) - y^1)   이렇게 됩니다. x^1 과 y^1 의 차이를 최소화 하는 것입니다.

x, y가 하나의 값이 아니기 때문에 여러 x(즉, x^(i))와 y(y^(i))에 대해서 누적 합계 계산이 필요합니다. 전체 훈련 데이터 예시 개수가 m 이므로 아래와 같이 정리가 됩니다.

J(θ) = 1/2  ∑ j=0,m ( h(xj) - yj )^2      (여기서 j는 훈련 데이터 예시의 인덱스)

이처럼 모든 훈련 데이터에 대한 전체 오차를 계산하는 함수 J(θ)를 코스트 함수(Cost function)이라고 합니다.  제곱으로 인해 일반적으로 값이 커지기 때문에 전통적으로 1/2로 값을 줄여준다고합니다. 그리고 오차 계산 시 왜 그냥 차이나 차이 절대값 등 다른 값을 안쓰고 제곱을 쓴 이유는 가우시안과 연계되어 있어서 라고하며 다음주에 더 자세히 말하겠다고 합니다.

이제 코스트 함수 J(θ)를 최소화하는 θ값을 찾기만 하면 좋은 모델을 만들 수 있습니다. 시작시 일단 θ를 모두 0 으로 정하고 모든 인풋 데이터 x에 대해서 h(x)를 계산하고 각각에 해당하는 y와의 차이를 제곱하여 J(θ)구할 수 있습니다.   그리고나서 θ값을 바꾸어가면서 가장 작은 J(θ)값을 찾으면 됩니다.  θ를 찾는 방법에 대한 설명을 위해 Gradient Descent를 설명합니다.

Gradient Descent

GD(Gradient Descent)를 아기 걸음에 비유하여 설명합니다. 그림과 같은 언덕(산)이 있을때 재일 위에 있는 검은 십자 표시에 아기가 서있고 제일 낮은 곳으로 가기위해 걸음을 걷는다고 생각해봅니다. 아기는 보폭에 해당하는 주위 360도를 둘러보고 제일 낮은 곳에 있는 것으로 보이는 방향으로 한걸음 옮김니다. 다시 이자리에서 주위 360를 돌아보고 제일 낮을 곳을 찾아 그쪽 방향으로 또 한걸음 옮김니다. 이렇게 계속하다보면 제일 아래쪽에 있는 검은 십자 표시에 다다른다고 설명합니다. GD의 특징으로 처음 시작점이 다르면 최종으로 다다르는 곳이 다를 수 있다는 것입니다. 

θ 값을 어떻게 바꿀 것인가? 방법을 GD로 사용했을 때 공식은 아래와 같습니다.

θj := θj - α  편미분(θj)   * J(θ)

α은 학습율(learning rate, 아기의 한 걸음 크기)이고, J(θ)를 시그마 σ가(전체합이) 아닌 1개의 테스트 데이터에 대해서 적용한다고 가정후 공식을 정리하면 아래와 같이 됩니다.

θj := θj - α ( hθ(x) - y ) * Xj

코스트 함수의 값이 커지면 학습이 안되고 있다는 것인데 문제의 이유중 하나가 학습 비율(Learning Rate)을 너무 크게 잡은 경우가 그럴 수 있습니다. 그래서 응 교수님은 두배씩 증가한 몇개의 학습 비율을 가지고(O2, O4, O8...) 테스트해 본다고 하십니다.

위 공식은 1개 태스트 데이터에 대해서 한것이고 이를 모든 훈련데이터에 적용하는 공식은 아래와 같습니다.

θj := θj - α  ∑ i=1,m ( hθ(x(i)) - y(i) ) * x(i)j   

(굵은 글씨 부분이 J(θ)를 θj로 편미분하는 것과 같은 부분입니다.,  j 는 피처의 순서로 예시의 경우 주택 크기와 방의 개수 데이터를 이용하므로 2 + 1(x0)이 되서 0부터 2까지가 됩니다.) 33:29

위 식을 말로 풀면 j번째 세타 값을 업데이트하는데 이 업데이트하는 값은 기존 세타 값에서 학습율과 편미분 값의 곱한 값을 빼서 구하는데, 이 편미분 값이란 모델이 출력한 값과 실제 값의 차이를 제곱한 값들의 합을 x의 값을 곱한 값을 모두 합친 값입니다.

이처럼 모든 훈련 데이터에 대해서 적용하는 Gradient Descent 방법을 Batch Gradient Descent라고 합니다.

좋은 질문과 답들이 나옵니다. 예를 들면 Batch GD가 더 정확한거 아닌가? 그런데 왜 실무에선 Stocastic GD를 많이 쓰나?, 언제 SDG를 중지해야 하나? 등입니다.

Normal Equation(정규 방정식)

선형회귀의 경우 이런 GD를 하지 않고도 바로 최소값을 알 수 있습니다. 이것이 Normal Equation(정규 방정식)입니다. 

이를 위해 함수와 행렬과 미분의 계산 방법을 설명해줍니다. 그리고 다양한 행렬 연산에 대한 기본 정의/특성을 설명해주고 숙제로 직접 증명해보라고 합니다.  이러한 행렬 연산을 이용하여 J(θ) 를 행렬간의 연산으로 바꿀 수 있다고합니다.

J(θ) = 1/2 ∑j=0, m  (h(xj)-yj)^2

        = 1/2 (Xθ - y)^T (Xθ - y)

미분θ * J(θ) = 1/2 미분θ (θ^T X^T - y^T) (Xθ - y)

= 1/2 미분θ [ (θ^T X^T Xθ) - (θ^T X^T y) - (y^T Xθ) + (y^T y) ]

= X^T Xθ - X^T y  =(set) 0백터

X^T Xθ - X^T y   "Normal Equation"

결국 찾고 싶은 값인 θ는 아래와 같은 공식으로 바꿀 수 있습니다. 

θ =  (X^T X)^-1  -  X^T y 

이렇게 하면 Gradient Descent 알고리즘을 통해 θ값을 찾지 않아도 X^T와 y를 이용해서 한번에 J(θ) 값을 제일 작게 만드는 θ값을 계산할 수 있습니다. 다시 말하면 J(θ)를 최소로 만드는 θ를 찾았다는 것은 가장 오차를 작게 만드는 θ를 찾은 것이므로 이값이 들어있는 모델(식)이 가장 좋은 모델이 되는 것입니다.  

내용이 좀 많고 행렬에 대한 이해가 조금 있어야 이해가되는 강의 입니다.  그럼에도 기계학습에서 감히 가장 중요하다고 할 수 있는 비용합수/로스함수 Cost Function(Loss Function)과 Optimizer(Gradient Descent)에 대한 내용을 설명해주는 좋은 강의 입니다.  아래에는 강의에 나오는 주요 용어에 대한 간단한 정의와 강의 링크입니다.

감사합니다.

Linear Regression(선형회귀)

통계학에서, 선형 회귀(線型回歸, 영어: linear regression)는 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀분석 기법이다.(소스: 위키피디아)

Batch/Stochastic Gradient Descent(SGD: 일괄/확률통계 경사 강하법)

SGD : 미분과 같은 연속적 특징을 가지는 목적 함수의 최적화를 위한 반복적인 방법의 하나이다.(소스: 위키피디아) Stochastic gradient descent (often abbreviated SGD) is an iterative method for optimizing an objective function with suitable smoothness properties (e.g. differentiable or subdifferentiable).

Normal Equation(정규 방정식)

정규방정식(Normal equation 혹은 Ordinary least squares 혹은 linear least squares)은 통계학에서 선형 회귀상에서 알지 못하는 값(parameter)를 예측하기 위한 방법론이다.(소스: 위키피디아)

강의 영상

https://www.youtube.com/watch?v=4b4MUYve_U8