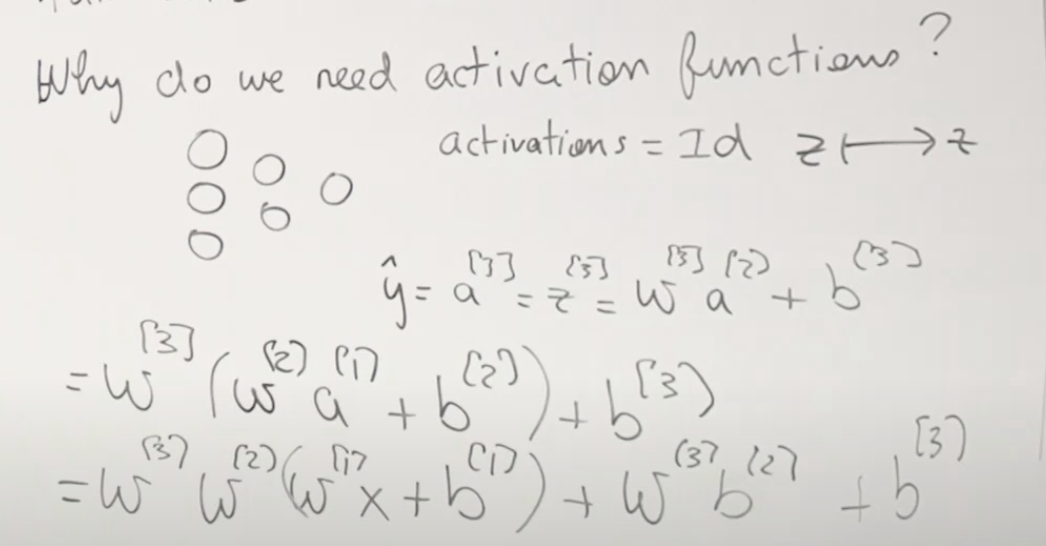The Yellow Lion King 데이터와 함께 살아가기

Lecture 13 - Debugging ML Models and Error Analysis | Stanford CS229: Machine Learning (Autumn 2018)

이번 강의의 주요 내용입니다.

오늘은 잘 동작하는 학습 알고리즘을 만들기 위한 조언에 대해 이야기 합니다.
오늘 자료는 깊이있는 수학적 내용은 아닙니다. 그러나 이번 수업에서 어찌보면 가장 이해하기 어려운 내용 중에 하나입니다. 과학과 예술 사이의 문제라고 할 수 있습니다. 어떤 사람들은 완전히 새로운 영역의 혁신적인 기계학습 연구를 할 때 이러한 조언들은 오히려 안 좋은 것이라고 말합니다. 그러나 기존에 연구된 유사한 문제를 유사한 방법으로 풀기위해서는 많이 도움되는 좋은 조언이라고 할 수 있습니다. 주요한 내용/아이디어는 다음과 같습니다. 1. 학습알고리즘을 디버깅하기 위한 진단방법은 무엇인가. 2. 에러 분석과 제거 분석은 무엇인가. 3. 기계학습 문제에서 통계적 최적화를 어떻게 시작할 것인가.

1. 학습알고리즘을 디버깅하기위한 진단방법은 무엇인가?

스팸 메일을 막기위한 Anti-spam 모델을 만든다고 가정해 보겠습니다. 모든 영어 단어를 피처로 이용하는 대신에 100개의 단어를 피처로 골랐습니다. 로지스틱 회귀와 경사 상향법을 가지고 모델을 구현하였습니다. 그래서 20%의 테스트 에러가 발생했는데 이것은 쓸수 있는 수준이 아닙니다. 자 이런 상황에서 여러분이라면 무엇을 하시겠습니까?

가장 기본적이고 효과적인 진단 방법은 바이어스/베리언스(bias vs. variance) 분석입니다. 무엇이 문제인지를 진단하고 그 문제를 고치는 방법입니다. 보통 모델의 성능이 좋지 않다고 하면 오버피팅이나 언더피팅일 경우입닌다. 오버피팅은 variance가 높은 경우를 말합니다. 반대로 언더피팅은 bias가 높은 경우를 말합니다. 예를 들면 스팸을 분류하기위해서 너무 작은 수의 피처가 사용되면 bias가 클 확률이 높아집니다. 이처럼 모델의 성능의 안정성을 진단하는 방법중 하나가 바로 variance와 bias를 알아보는 것입니다. variance가 큰 경우는 훈련 에러가 테스트 에러보다 훨씬 작은 경우에 발생 합니다. 즉, 훈련에서는 잘 맞추는데 테스트에서는 못 맞추는 경우 입니다. Bias가 큰 경우는 훈련 에러와 테스트 에러가 모두 높은 경우 입니다. 아무리 훈련해도 에러를 줄이지 못하는 상황이 많습니다.

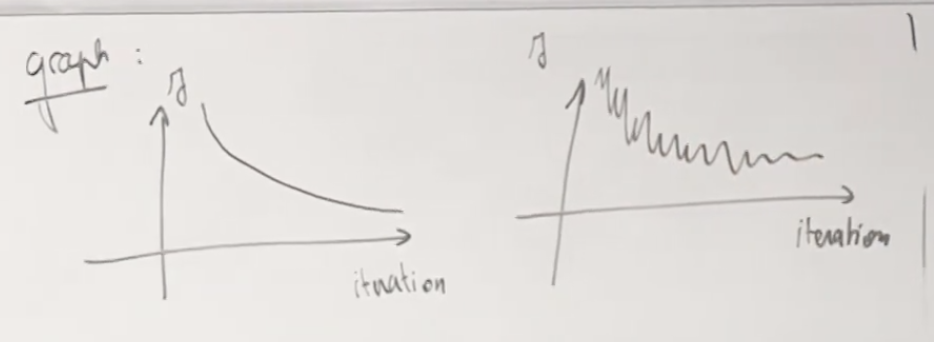
높은 variance를 가지는 모델의 에러와 데이터 량을 그래프로 그려보면 아래와 같습니다. 데이터 수가 많아져도 훈련 에러율과 테스트 에러율의 차이가 계속 발생하고, 훈련 때는 원하는 에러율보다 낮지만 테스트 할때는 높습니다. 그리고 테스트에서는 원하는 목표 에러율보다 낮아지지 않습니다. 목표에러와 테스트 에러의 차이가 많이 난다는 의미입니다. 데이터(m)가 늘어 남에 따라서 테스트 에러율이 낮아지고 있으므로 더 많은 데이터가 도움이 될 것 입니다. 그럼에도 불구하고 훈련 에러율과 테스트 에러율 사이에 차이가 있습니다. 높은 Variance가 있을 경우 아래와 같은 그래프를 보입니다.

다음은 높은 bias를 가진 러닝 커브의 예를 들어 보겠습니다. 높은 바이어스가 있는 경우 훈련 에러와 테스트 에러는 데이터가 많아 짐에 따라서 비슷해지지만, 심지어 훈련 에러율도 원하는 에러율 보다 않좋게 나오는 경우 입니다. 훈련이 잘 안되는 거죠. 이런 경우에는 아무리 많은 데이터 사례를 더 모아서 훈련해도 원한는 모델을 만들 수 없습니다.

Bias-variance is the single most powerful tool for analyzing the performance of a learning algorithm.
guess some problems and find out whether the model has the problems or not.

일반적으로 많이 연구되지 않은 새로운 영역의 모델을 만들때 추천하는 방법은 먼저 지저분한 코드라도 빠르게(Quick and dirty code) 만들어서 돌려보고 Bias/Variance 진단을 해보는 것입니다.



앞서 살펴본 Bias / Variance 문제가 가장 흔하고 가장 중요한 진단 방법입니다. 그밖의 다른 문제에 대해서는 무엇이 잘못된 것인지를 알아내기 위한 당신의 진당방법을 만들기위한 당신의 창의성에 달려있습니다. 다른 예를 들어 보겠습니다. 로지스틱 회귀 모델을 통해 스팸 메일에 대해 2%의 에러율과 정상 메일에 대해 2%의 에러율을 얻었다고 합시다. 실제로 사용하기 어려운/받아들이기 힘든 수준입니다. 또 다른 성형 커널 기반의 SVM 모델을 이용해서 스팸 메일에 대해서 10%의 에러율을, 정상 메일에 대해서 0.01%의 에러율을 얻었습니다. 이정도 성능은 받아들일만 하다고 하겠습니다. 그런데 당신은 계산의 효율성을 위해서 로지스틱 회귀 모델을 사용하기를 원합니다. 어떻게 해야할 까요? 

다른 일반적인 질문중 하나는 '알고리즘이 수렴하고 있는가?' 입니다. 오브젝티브 함수를 지켜봄으로써 알고리즘이 수렴하고 있는지를 말하기 어려운 경우가 종종 있습니다. 일반적으로 훈련 반복을 늘리면 오브젝티브 함수는 조금씩 올라가게 됩니다. 그런데 얼마나 더 많은 반복을 해야할까요? 더 많은 반복이 효과적일지 아닌지 어떻게 알까요? 보다 체계적인 방법이 없을까요? 

아마도 무엇이 잘 못 되었는지 생각해 본다면 다음과 같은 질문을 할 수 있습니다. 최적화를 위해 올바른 함수를 사용하고 있는가? , 로지스틱 회귀가 맞나? 학습률은 적절한가? 등이 그것 입니다.

SVM은 보통 로지스틱 회귀를 능가하는 성능을 보입니다. 그러나 여러분은 어플리케이션을 위해서 로지스틱 회귀 모델의 배포를 원하는 상황입니다. SVM의 성능이 BLR을 능가함으로, 가중치를 적용한 SVM과 BLR의 정확도를 비교하면 a(θ SVM)이 더 커야 합니다.

BLR 베이지안 선형회귀 (위키피디아)
In statistics, Bayesian linear regression is an approach to linear regression in which the statistical analysis is undertaken within the context of Bayesian inference. When the regression model has errors that have a normal distribution, and if a particular form of prior distribution is assumed, explicit results are available for the posterior probability distributions of the model's parameters.
https://en.wikipedia.org/wiki/Bayesian_linear_regression

베이지안 회귀 분석 https://mons1220.tistory.com/212

먼저 최적화 알고리즘의 문제가 있으면 경사하강법은 수렴하지 않을 수 있습니다. 두번째로 잘못된 비용함수를 이용하면 학습되지 않을 수 있습니다.
즉, 진단해야할 것은
1. 옵디마이징 알고리즘이 잘못되서 수렴하지 못하는 건지
2. 아니면 비용함수를 잘못 만든 것인지
확인이 필요합니다.
로지스틱 회귀가 최대화 하려는 비용함수를 확인해볼 필요가 있습니다.

이를 위한 진단 방법은 아래와 같습니다. 앞서본 정확도 a(θ)와 비용함수 J(θ)를 가지고 무엇이 잘못된 것인지 진단 할 수 있습니다. 

케이스1 의 경우는 최적화 알고리즘에 문제가 있는 경우이고, 케이스2의 경우는 비용함수가 문제인 경우입니다.

그래서 앞서 살펴 봤던 여러 개선 방법들 중에서 최적화 알고리즘의 문제를 해결하기 위한 방법들과 비용함수 문제를 해결하기 위한 방법들이 아래와 같이 매칭 됩니다.

SVM을 시도하는 것도 오브젝티브 함수를 최적화 하는 것을 고치기 위한 방법중 하나 입니다. 

Debugging an RL algorithm

강화학습에 대한 상세 내용은 별도로 정리하겠습니다.

Error Analysis

일반적인 얼굴인식 시스템의 절차는 다음과 같습니다.

원본 사진에서 배경을 지우고

얼굴을 찾고

얼굴에서 눈, 코, 입을 찾고

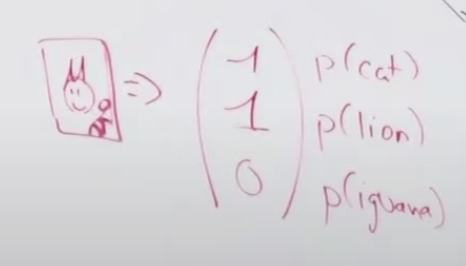
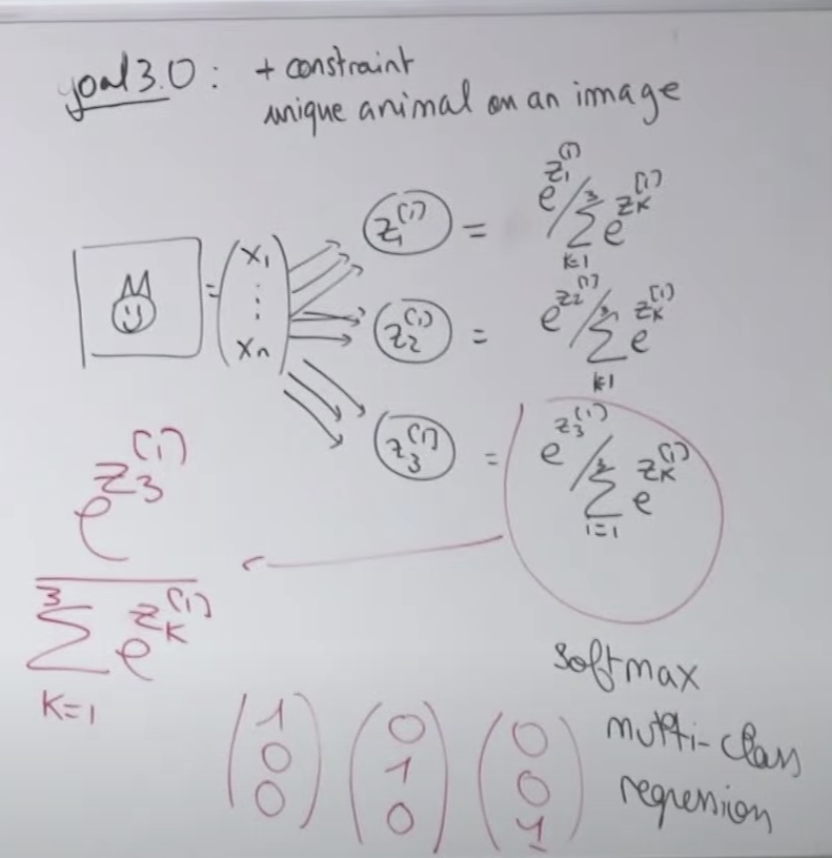
모델(로지스틱 회귀)을 실행시켜서 최종 아웃풋 레이블을 만듭니다.

전체적인 플로우는 다음과 같습니다.

따라서 각각의 단계 / 모듈이 오류율을 어떻게 변화하는지를 확인할 수 있습니다.

Ablative analysis

Ablative analysis는 각 콤포넌트가 최종 성능에 각각 얼마나 기여했는지를 측정하는 방법입니다. 좋은 피처들이 없는 단순 선형 회귀 모델을 통해서 94%의 성능이 나오고 콤퍼넌트를 추가했을 때 99.9%로 모델 성능이 향상 된 것을 어떻게 설명할 것인가? 라는 질문에 대답할 수 있는 방법이 Ablative analysis입니다. 즉, 기본 베이스 라인 모델(94%)에서 시작해서 하나씩 콤퍼넌트가 추가될때 마다 성능(Accuracy)이 어떻게 변하는지 확인하는 방법입니다. 이런 Ablative analysis를 통해서 어떤 콤퍼넌트가 성능향상에 가장 기여를 많이 하는지 알수 있습니다.

아래는 강의 동영상 링크 입니다.
https://www.youtube.com/watch?v=ORrStCArmP4

주요내용

• One-hot Encoding 이란?
• 왜? 원핫 인코딩이 필요한가?
• 어떻게 하나?
• 장점 및 단점
• 파이썬에서의 구현 방법

One-hot Encoding 이란?

먼저 위키피디아에 따르면 One-hot 을 아래와 같이 정의하고 있습니다.

A one-hot is a group of bits among which the legal combinations of values are only those with a single high (1) bit and all the others low (0).

즉, 비트 들의 모임 중 하나만 1이고 나머지는 모두 0인 비트 들의 그룹을 원핫(One-hot)이라고 합니다. 

그럼 인코딩(Encoding)이란 무엇일까요? 인코딩은 부호화라는 의미로 위키피디아에서는 아래와 같이 말하고 있습니다.

인코딩(encoding)은 컴퓨터를 이용해 영상 · 이미지 · 소리 데이터를 생성할 때 데이터의 양을 줄이기 위해 데이터를 코드화하고 압축하는 것이다.

 쉽게 말하면 데이터를 압축/변형 하는 것은 인코딩, 이 압축/변형된 데이터를 원형으로 변환하는 것을 디코딩(Decoding)이라고 합니다.  

그래서 원핫과 인코딩을 합친 One-hot Encoding(원핫 인코딩)이란

데이터를 One-hot 데이터 형태로 변형/압축하는 것

을 말합니다. 여기서 데이터는 이미지 데이터가 될 수도 있고 텍스트 데이터나 카테고리(범주형) 데이터가 될 수도 있습니다. 

왜? 원핫 인코딩이 필요한가?

일반적인 인코딩은(부호화는) 정의에서 나온 것처럼 변형하거나 압축이 필요할 때 사용됩니다. 복잡하고 긴 이름이나 내용을 특정 규칙에 따라 변형 또는 매핑하여 축소할 때 효과적입니다. 파일 압축을 생각해보세요. 메일이나 메신저를 사용해서 용량이 큰 이미지나 동영상 파일을 전송할때 생각해보세요. 그냥 전송하는 것보다는 압축한 파일을 전송하는 것이 훨씬 빠르고 안정적입니다. 이처럼 원핫 인코딩의 경우에도 복잡한 데이터를 그대로 사용하지 않고 컴퓨터가 처리하기 쉽게 숫자로 변형해 주는 것입니다. 이렇게 함으로써 데이터를 처리하기 위해 필요한 메모리 양을 줄일 수 있고 처리를 빠르게 할 수 있습니다. 게다가 대부분의 통계나 머신러닝 모델들은 입력 데이터로 숫자값을 기본으로 합니다. 그래서 특히, 범주형 데이터를 원핫 인코딩해서 사용하는 경우가 많이 있습니다. 예를 들어서 주택 데이터 셋 중에서 주택 유형이라는 피처(데이터 항목)이 있고 이 항목의 실제 값들은 '아파트', ''연립주택', '다세대주택', '단독주택', '다중주택', '다가구주택', '기타' 로 구성되어있다고 하겠습니다. 이러한 값들을 그대로 모델의 입력값으로 사용할 수 없기 때문에 숫자로 바꾸어주는 것이 필요합니다. 그래서 이 법주형 데이터를 원핫 인코딩으로 변환할 경우, '아파트'는 '100000'으로 '연립주택'은 '010000'으로 변환되어 사용될 수 있습니다. 이렇게 원핫 인코딩된 값들은 분석 모델의 인풋 데이터로 사용할 수 있습니다. 

어떻게 하나?

방법은 간단합니다. 범주형의 종류 개수(n) 크기의 벡터를 0으로 초기화하고, 특정 범주를 나타내기 위해 특정 위치의 값을 1로 설정하는 것 입니다. 위의 예에서도 잠깐 살펴본 주택 데이터 셋 예를 더 자세히 알아보겠습니다.  주택 유형이라는 범주형 데이터의 전체 범주 개수가 6개인 경우 벡터의 크기는 6이 됩니다. 이 벡터를 리스트로 표현하면 [0,0,0,0,0,0]이 됩니다. 크기가 6인 0벡터 이지요. 첫번째 범주인 '아파트'를 원핫 인코딩해보면 [1,0,0,0,0,0]로 나타 낼 수 있습니다. 첫번째 위치 값을 1로 설정하고 나머지는 모두 0인 원핫 벡터가 되었습니다. 다른 범주값까지 모두 원핫 인코딩 한 결과는 아래와 같습니다.

장점 및 단점

장점은 어떻게 인코딩/디코딩 되는지 쉽게 이해할 수 있다는 것 입니다. 구현도 쉽고 작은 데이터 셋에서 빠르게 동작한다는 장점이 있습니다.

단점은 범주가 추가되면 데이터의 크기가 바뀐다는 것입니다. 위에서 주택유형을 입력으로 쓰기 위해 6자리의 원핫 벡터로 인코딩해서 사용중이었는데 예를들어 전원주택 같은 새로운 주택유형이 하나 추가되면 7자리의 벡터로 바꾸어서 사용해야한 다는 것입니다. 이 말은 기존에 만들었던 모델이나 알고리즘에 변형이 필요하다는 의미 입니다. 매우 큰 변화이지요. 이처럼 향후의 확장성을 고려하여 더미 범주를 추가해서 인코딩하거나 해싱을 이용해서 인코딩 하기도 합니다. 이러한 문제를 OOD(Out Of Dictionary) 라고도 합니다. 예측이나 추론을 위해 원핫 인코딩을 실행했는데 모델이나 알고리즘을 개발할때에는 없던 새로운 범주가 입력되는 경우 인코딩 할 수 없어서 발생하는 에러를 말합니다.

정보저장을 위해 희소 벡터(Sparse Vector)를 사용하기 때문에 정보가 없는 공간에 대해서도 관리가 필요하게 되어서 메모리의 낭비가 발생한다는 것입니다.  위의 주택 유형 예에서 '아파트'를 '100000'으로 인코딩하면 첫번째 1만 값이 있고 나머지는 위치는 모두 정보가 없는 0이 차지하기 때문에 메모리 낭비가 발생하는 것입니다.

또 다른 단점은 범주형 데이터가 순서나 크기의 의미를 포함하고 있을 때 원핫 인코딩을 하게되면 이러한 정보들은 사용할 수 없게된다는 것입니다. 예를 들면 월요일, 화요일, 수요일, 목요일, 금요일, 토요일, 일요일을 원핫 인코딩하면 그저 0과 1일 집합으로 표현됩니다. 월요일은 [1,0,0,0,0,0,0], 토요일은 [0,0,0,0,0,1,0], 일요일은 [0,0,0,0,0,0,1] 이렇게 되겠지요. 이렇게 인코딩된 값들은 요일간에 순서나 크기를 표현하지 못합니다. 반면에 레이블 인코딩의 경우 일요일은 0, 월요일은 1, 화요일은 2, 수요일은 3, 목요일은 4, 금요일은 5, 토요일은 6으로 인코딩하면 요일간의 연계성 정보를 인코딩한 숫자에서도 찾을 수 있습니다. 즉, 수요일 3 다음에는 목요일 4라는 것을 알수 있지요. 이렇게 되면 5보다 큰 수가 의미를 갖을 수도 있습니다. 

파이썬에서의 구현 방법

원핫 인코딩은 통계, 기계학습, 머신러닝, 딥러닝 등 쓰이는 범위가 넓습니다. 그래서 원핫 인코딩 기능은 여러 프레임웍과 페키지에서 제공하고 있습니다.  아래는 scikit-learn 패키지에서 구현한 예시 내용입니다. 

# scikit-learn에서 필요한 모듈을 가져옵니다.
from sklearn.preprocessing import OneHotEncoder

# 프로그램에서 사용할 인스턴스를 하나 만듭니다.
one_hot_encoder = OneHotEncoder()

# 데이터 셋에서 범주형 데이터 항목의 값들을 인코더의 입력값 X로 설정 합니다.
X = [['Apple'], ['Banana'], ['Cherry'], ['Date'], ['Egg'], ['Apple'], ['Cherry'], ['Cherry']]
print('데이터 항목 X: ', X)

# 데이터 X를 이용해서 one hot encoding을 적용 실행
one_hot_encoder.fit(X)

# 인코딩된 카테고리들의 내용을 확인해 보는 명령어
categories = one_hot_encoder.categories_
print('범주 categories: ', categories)

# 특정 범주(여기서는 'Apple', X[0])에 해당하는 원핫 벡터를 찾아보는 명령어
one_hot_vector_for_alpha = one_hot_encoder.transform([X[0]]).toarray()
print('Apple를 인코딩한 값(벡터): ', one_hot_vector_for_alpha)

# 특정 원핫 벡터(여기서는 'Apple'의 원핫 벡터 [[1. 0. 0. 0. 0.]])에 해당하는 범주 Category를 찾는 명령어
category_for_one_hot_vector = one_hot_encoder.inverse_transform(one_hot_vector_for_alpha)
print('Apple 인코딩 벡터를 이용해서 찾은 범주 이름: ', category_for_one_hot_vector)

print('\n모든 범주와 원핫 인코딩을 출력 합니다.')
for category in one_hot_encoder.categories_[0]:
    print(category,': \t', one_hot_encoder.transform([[category]]).toarray())

위의 내용을 실행하기 전에 pip install sklearn 명령을 통해 scikit-learn 패키지를 설치해 주어야 합니다. 아래는 패키지를 설치하고 위의 내용을 파일로 저장후 실행한 결과 입니다.

데이터 항목 X: [['Apple'], ['Banana'], ['Cherry'], ['Date'], ['Egg'], ['Apple'], ['Cherry'], ['Cherry']]
범주 categories: [array(['Apple', 'Banana', 'Cherry', 'Date', 'Egg'], dtype=object)]
Apple를 인코딩한 값(벡터): [[1. 0. 0. 0. 0.]]
Apple 인코딩 벡터를 이용해서 찾은 범주 이름: [['Apple']]

모든 범주와 원핫 인코딩을 출력 합니다.
Apple :    [[1. 0. 0. 0. 0.]]
Banana : [[0. 1. 0. 0. 0.]]
Cherry :  [[0. 0. 1. 0. 0.]]
Date :      [[0. 0. 0. 1. 0.]]
Egg :       [[0. 0. 0. 0. 1.]]

요약

원핫 인코딩이 무엇인지에 대해서 알아보았고, 왜필요한지, 그리고 어떻게 구현할 수 있는지에 대해서 알아보았습니다. 이렇게 인코딩된 데이터를 이용하여 분석하거나 머신러닝 모델에서 입력 값으로 사용할 수 있습니다. 위에서 보신 것 처럼 Apple을 모델에서는  [[1. 0. 0. 0. 0.]]로 입력 받아 처리합니다. 결과 값을 분류하는 경우, 즉 과일 이름 중에 하나가 결과로 나와야하는 경우에는 역으로  [[1. 0. 0. 0. 0.]]로 나온 모델의 결과 값을 다시 'Apple' 로 바꾸어주는 것이 필요합니다. 이처럼 원핫 인코딩/디코딩은 범주형 데이터의 변환에 많이 쓰입니다. 

주요 내용

• Backprop - 백프로파게이션(역전파)
• Improving Neural Networks - 신경망을 더 개선시키는 방법
  • Activation Function - 활성화/활성 함수
  • Initialization Methods - 초기 웨이트 설정 방법
  • Optimization - 최적화 방법

업데이트를 할때 미분을 하는데 이때 아웃풋에 제일 가까운 레이어(w[3]) 부터 미분하는 것이 계산하기 좋다는 것 까지 지난 시간에 이야기 했습니다.

Backprop(역전파)

역전파, 백프로파게이션, Backprop을 해 보겠습니다.  w[3]부터 계산합니다. J (Cost Function)의 값을 w[3] 값으로 미분합니다.

이렇게 계산을 진행하기 위해서는 사실 먼저 알아야할 전제사항/공식이 있는데요 아래와 같습니다.

J를 w[3]로 미분하는 위에 위에 있는 이미지에서, 마지막에 a[2]에 왜 Transpose 를 할까요? 바로 행렬간의 계산을 할 수있도록 해주기 위해서 입니다. 아래에서 처럼 transpose를 해주어야 (1, 2) 행렬이 됩니다.

계속 풀어보면 다음과 같습니다.

이것을 m개의 훈련 데이터에 대해서 평균을 내는 것은 아래와 같습니다.

w[3]에 대한 계산이 끝났으니 그 이후에는 w[2]에 대한 미분입니다. 어떻게 하면 더 효율적으로 계산할 수 있을까요? 

로스 함수를 w[3]로 미분한다는 것은 아래의 오른쪽 내용 처럼 분리가 가능한데요.. 이 내용을 자세히 보면 이전에 구했던 왼쪽의 내용에서  변형할 수 있는 값을 유추할 수 있습니다. 바로 a[2]T가 z[3]를 w[3]로 미분한 것과 같다는 것 입니다.

그래서 w[2]로 미분하는 공식에 대하여 동등한 내용을 빨간색으로 표시해 보면 아래와 같습니다.

그래서 동등한 내용으로 재 정리하면 아래와 같습니다. 그런데 중간에 행렬의 크기가 일치하지 않아서 행렬 연산이 안되기 때문에 Elementwise dot (모든 요소간의 곱)이 필요합니다. 그렇게 해서 행렬의 크기를 동일하게 맞출 수 있습니다.

상기 내용을 어떻게 프로그래밍 해야할지 걱정하지 않아도 됩니다. 많은 머신러닝 프레임웍에서 이런 계산을 대신해 주기 때문입니다.

포워드 프로파게이션을 하는 동안 계산 내용을 모두 메모리에 저장해 놓았다가 백워드 프로파게이션 시에 사용함으로써 메모리 사용을 줄이고 계산 속도를 높일 수 있습니다.

Imporving Neural Networks

A) Activation Function

지금까지 배운 내용으로 신경망을 만들고 훈련해도 만족할 만한 성과를 못 얻을 수 있습니다. 그래서 더 좋은 성능을 내는 신경망을 어떻게하면 만들 수 있는지에 대해서 알아보겠습니다.

제일 먼저 가능한 것은 Activation Funcion(활성화 함수)을 바꾸는 것 입니다.

시그모이드 함수나 탄젠트h 함수는 z 값이 아주 커지거나 작아지면 출력값의 차이가 작아져서 w를 업데이트 하는 영향이 거의 없어집니다. 즉, gradient vanishing 문제를 발생하게 됩니다. ReLu는 이런 문제를 해결하는 함수 입니다.

그럼 왜 활성화 함수가 필요할 까요?

위의 두 이미지에서 보면 알 수 있듯이 활성화 함수가 없다면 네트워크의 깊이가 아무리 깊어도 선형 함수의 분류기와 같을 뿐입니다.  

보통 같은 레이어에서는 같은 활성화 함수를 이용합니다. 다른 레이어에는 다른 활성화 함수를 사용할 수 있습니다. 위에서 살펴본 시그모이드 함수(Sigmoid), 레루 함수(ReLu), 탄젠트h 함수(tanh) 이외에도 여러가지가 있지만 기본적인 함수는 이 정도가 됩니다.

B) Initialization Methods

두번째로는 초기화 방법에 대해서 알아보겠습니다. 아래 이미지는 평균으로 정규화할 경우 변화되는 내용을 설명합니다.

표준편차를 통해 정규한 내용이며 이럴 경우 최적값을 찾아가는 경로가 훨씬 단축되게 됩니다. 그래서 정규화를 하는 것이지요.

상기에서 사용한 평균이나 표준편차는 모두 훈련 데이터에서 계산된 것을 말하며 이것은 테스트 시에도 동일한 값을 이용해서 계산되야 합니다.

베니싱 그레디언트(Vanishing Gradient)에 대해서 좀더 자세히 알아보겠습니다. 아래와 같이 히든 레이어가 10개, 활성화 함수는 Identical 함수(그냥 통과하는 함수), 그리고 바이어스는 0인 신경망을 만들었다고 하겠습니다. 아래 계산에서도 볼 수 있듯이 w 의 값이 초기값에 L 승으로 곱한 결과가 됩니다. 따라서 초기 값이 1보다 조금만 커도 결과 값은 아주 큰 값으로 설정이 되고 1보다 작은 값을 설정을 해도 결과 값은 아주 작은 값으로 설정되게 됩니다. 0.9, 1.1 처럼 1 근처의 값으로 주면 그나마 변화량이 덜 할 것입니다. 그러나 조금만 커져도 엄청낙게 큰 값으로 바뀌고 조금만 더 작아져도 엄청나게 작은 값으로 바뀝니다. 그래서 활성화 함수가 중요합니다.

하나의 뉴런을 가지고 예를 들어보겠습니다. 보시는 것처럼 n이 커지면 w(i)가 작아집니다.  따라서 w(가중치)의 초기 값을 1/n으로 설정하는 것도 좋은 가중치 초기화 방법 중에 하나 입니다.

그래서 시그모이드 활성화 함수에 대해서는 아래와 같은 코드로 초기화 하는 것이 동작을 잘 합니다.

다른 초기화 방법으로 Xavier Initialization(자비어 초기화)이 있습니다.

C) Optimization

세번째 방법으로 옵티마이제이션에 대해서 알아보겠습니다.

아래는 이렇게 배치로 최적화 할때랑 아닐때랑을 비교한 비용함수 곡선입니다.

배치 그레디언트 디센트(Batch Gradient Descent) 방법을 2차원에서 그려보면 아래의 녹색 선과 같이 움직입니다. 이상적인 빨간색 경로보다는 돌아가는 것 같지만 하나의 이터레이션을 훨씬 빠르게 실행할 수 있습니다.

또 약간 다른 Gradient Descent와 Momentum(모멘텀) 알고리즘을 소개합니다. 일반적으로 GD를 쓰면 빨간색 선과 같이 움직이면서 최적값을 찾아가는데, 여기에 모멘텀을 더하면 녹색 선과 같이 움직이게 됩니다. GD는 지나온 과거의 움직임을 고려하지 않고 앞으로 나아 갑니다. 반면에 모멘텀은 과거 움직임을 고려해서 앞으로의 방향을 조정합니다. 처음 시작점에서 두번째 점으로 이동했을때 가로, 세로의 변화량을 보면 세로의 변화량은 큰데 가로의 변화량은 작습니다. 이것을 눈치첸 모멘텀은 가로를 더 많이 가게 조정해서 녹색 선의 세번째  점을 향하게 됩니다. 이런 방법으로 학습하면 훨씬 더 빠르게 최적화를 할 수 있습니다.  

모멘텀의 구현방법은 아래와 같습니다.

물론 이러한 방법은 기본적인 내용이며, 이 밖에도 많은 최적화 방법이 있습니다. 그 중에서 특히, Adam과 RMSProp은 신경망에서 많이 쓰이는 최적화 방법들이 있습니다. 

아래는 강의 동영상 입니다.

https://www.youtube.com/watch?v=zUazLXZZA2U&list=PLoROMvodv4rMiGQp3WXShtMGgzqpfVfbU&index=13 

주요 내용

• Deep Learning 이란
• Linear Regression 으로 본 신경망
• Neural Networks

Deep Learning  이란

딥러닝은 머신러닝의 한 분야로 특히 컴퓨터비전(CV), 자연어처리(NLP) 등에 많이 사용 되는 알고리즘 입니다. 새로운 처리 방법이지요.

딥러닝이 잘 동작하는 이유는 다음과 같습니다.

새로운 처리 능력의 향상: 첫번째 이유는 계산에 많은 비용이 드는 알고리즘 입니다. 많은 계산이 필요해서 병렬처리하는 것이 필요했는데 GPU가 사용 되었습니다. 많은 계산을 빠르게 처리할 수 있게된 것이지요. 

많은 데이터 : 인터넷 활성화에 따른 많은 데이터가 만들어 졌고 이렇게 많은 데이터를 가지고 모델을 만들 수 있게 되었습니다. 딥러닝 모델을 데이터가 다 많으면 많을 수록 더 잘 학습하게 됩니다.

새로운 알고리즘 : 많은 데이터와 새로운 계산 처리 기술을 이용하는 새로운 알고리즘을 만들어 냈습니다.

Logistic Regression 으로 본 신경망

첫번째 목표

지난 시간에 배운 로지스틱 리그리션을 활용해서 신경망을 설명해 보겠습니다. 첫번째 분류 문제로 고양이가 들어있는 이미지를 분류하는 것을 생각해 보겠습니다. 고양이가 있으면 1, 없으면 0을 나타내는 모델을 만들어 봅시다.  컴퓨터 공학에서 이미지를 3차원 행렬로 표현합니다. RGB 3가지 채널이 있기 때문이지요. 가로64픽셀, 세로 64픽셀의 칼라 이미지가 있다면, 가로 64픽셀 X 세로 64픽셀 X 3(RGB) 개의 픽셀 값으로 표현 됩니다. 이 값들을 하나의 벡터로 만들어서 입력 데이터로 사용합니다. 로지스틱 회귀에서의 공식을 적용해보면 아래와 같이 됩니다. 각 입력값 별로 가중치가 필요하니 64 * 64 * 3 개의 w가 필요합니다. 그래서 W의 크기가 (1, 12288)이 되었습니다.

모델을 훈련하는 절차는 다음과 같습니다. i) 먼저 w(가중치), 와 b(바이어스) 를 초기화 합니다.  ii) 최적의 w, b를 찾습니다. iii) 찾은 w,b 값을 이용해서 모델을 통해 예측을 실행 합니다. 두번째 단계가 특히 중요한데 여기서 로스(loss)와 Optimizer(Gradient descent) 같은 방법을 사용해서 최적의 w, b를 찾습니다. 로스는 MLE 를 이용해서 구하고 w와 b는 편미분한 값을 빼줌으로서 학습합니다.

여기에 사용되는 파라메터 갯수는 모두 몇개일 까요? 

바로 12,288개 + 1개 입니다. 즉, 웨이트 갯수와 바이어스 갯수의 합인 것이지요. 

두가지 기억하고 있어야 할 것이 있습니다. 첫째, 뉴런은 리니어 파트와 엑티베이션 파트로 구성된다는 것 입니다. 위의 그림에서 wx + b 부분이 리니어 파트이고 시그마 부분이 엑티베이션 파트 입니다. 동그라미가 바로 뉴런 입니다.  두번째, 모델은 아키텍처와 파라메터라는 것 입니다. 실무에서 모델을 만들어 배포했다는 것은 모델 아키텍처파일과 파라메터 파일을 배포했다는 것이고 이 두 파일을 이용해서 예측을 계산 / 실행하게 됩니다. 

두번째 목표

두번째 분류 문제를 생각해 보겠습니다.  이번에는 이미지에서 고양이, 사자 또는 이구아나를 찾는 문제 입니다. 어떻게 할 수 있을까요? 뉴런을 2개 더 만들어서 3개로 할 수 있겠습니다. 

그럼 이 모델에서는 몇개의 파라메타가 있을가요?  앞에서 소개한 파라메터 숫자의 3배가 필요합니다.  

그럼 어떤 데이터가 필요할까요?  네..이미지 데이터와 레이블 데이터 입니다. 이번 문제에서는 고양이, 사자, 이구아나 중에 어떤 동물인지를 표시해야하기 때문에 레이블 데이터가 필요합니다. 1번 이미지는 고양이 이고, 2번 이미지는 사자이고 등등...여기서 고양이, 사자 이런게 레이블 데이터 입니다. 즉, 레이블 데이터이란 훈련 데이터에 해당하는 정답 데이터를 말합니다. 이미지도 숫자로 입력되는 것처럼 출력도 고양이, 사자 이렇게 할 수 없어서 숫자나 위치를 정해야합니다. 이번 문제에서는 아래와 같이 레이블 데이터를 정하겠습니다. 하나의 이미지에 대해서 하나의 벡터 값으로 어떤 동물인지를 표시하는 것 입니다. 예를 들어 첫번째 값이 1이면 고양이를 표시하고, 두번째 값이 1이면 사자, 세번째 값이 1이면 이구아나를 의미합니다.

위와 같은 데이터를 가지고 모델을 훈련할 수 있습니다.  w, b를 초기화 시키고 로스를 계산하고 오차를 계산해서 w,b를 변경해 가면서 최적의 모델을 만들 수 있습니다.

이렇게 진행할 경우 그림 3에 제일 위에 있는 첫 번째 뉴런은 무엇을 배울까요?   바로 이미지에 고양이가 있는지 없는지를 학습하게 됩니다. 왜 그럴까요?  바로 아웃풋의 첫번째 위치가 바로 고양이의 존재 여부를 판단하는 내용이고 이 아웃풋이 첫번째 뉴런과 연결되어 있기 때문입니다. 아웃풋 벡터의 순서가 다른 것을 의미한다면, 즉 레이블 데이터가 바뀐다면 각 뉴런에서 학습하는 내용은 바뀌게됩니다.

그럼 이 모델은 여러 개의 동물이 있는 이미지에도 잘 분류할까요? 만약, 고양이와 사자가 들어있는 이미지를 모델에게 준다면 모델은 고양이도 잇고 사자도 있다고 판단할 것입니다. 아래 그림처럼 아웃풋 벡터에서 고양이와 사자에 해당하는 위치의 값이 1로 나올 것 입니다.

로스 계산은 아래와 같습니다. 각 동물별 로스의 합으로 전체 로스를 만듭니다.

세번째 목표

문제 3 세번째는 2번째 문제에서 처럼 두가지 동물을 모두 표시하는 것이 아니라 하나의 이미지에 가장 확실한 동물 한 종류만 표시하고 싶습니다. 어떻게 해야할 까요?  각 동물에 해당하는 출력 값들을 모아서 각 동물의 결과를 나누어 주면 됩니다. 그러면 각 동물별 결과치의 비율이 나오게 됩니다. 각 비율을 모두 합친 값은 1이 되겠지요. 에를 들면 처음 z1, z2, z3 값이 5, 3, 1 이었다면 소프트맥스 함수를 거쳐서 나온 값은 [0.86681333 0.11731043 0.01587624]이 됩니다. 결과 값이 z1이 제일 크네요. 이렇게 만드는 것이 소프트맥스(Softmax) 함수 입니다.  이러한 결과 값과 비교하기 위해 레이블 데이터는 고양이인 경우 [1,0,0], 사자인 경우 [0,1,0], 이구아나인 경우 [0,0,1] 로 등록되야 합니다. 이처럼 소프트맥스 함수를 통해 출력의 분포를 구할 수 있습니다.

Softmax 함수 계산으로 출력값 z1, z2, z3사이에 서로 영향을 주기 때문에 로스는 크로스엔트로피로스(Cross Entropy Loss)를 이용합니다.

질문입니다. 만약 이미지에서 고양이의 존재를 있고 없고 판단하는게 아니라 고양이의 나이가 얼마가 되는지를 예측하는 문제라면 어떤 네트워크를 사용하시겠습니까?  문제 1을 풀기 위한 그림1 네트워크가 좋을까요?, 문제 2를 플기위한 그림3의 네트워크가 좋을 까요? 아니면 문제 3을 풀기위한 그림5의 네트워크가 좋을까요? 네 문제 3을 풀기위한 그림5 네트워크를 연령대 구분으로 나누어서 사용할 수 있을 것 같습니다. 첫번째는 10대, 두번째는 20대...이런 식으로요...물론 하나의 출력 노드를 가지는 리그레션 모델로 만들 수도 있습니다. 리그레션 모델로 한다면 시그모이드 함수를 사용하지 말아야 겠지요. 그 대신 신경망에서 많이 사용하는 레루 ReLU 함수를 이용하는 것이 좋습니다. 로스함수는 L1 놈/노름( |y^ - y|) 또는 L2 놈/노름(||y^ - y||L^2)를 사용하면 되겠습니다.

Neural Networks

다시 이미지에 고양이가 있는지 없는지를 구분하는 첫번째 문제를 생각해 보겠습니다. 로지스틱 회귀의 신경망 버전에서와 달리 중간에 히든 레이어를 추가할 수 있습니다. 이것은 입력과 출력에서 보이지 않는 신경망 계층을 의미합니다. 신경망의 첫번째 레이어는 단수한 엣지 같은 것을 식별해내고 두번째 레이어에서는 귀나 입 같이 좀더 복잡한 모양을 찾아냅니다. 이처럼 신경망의 깊이가 깊어질 수록 보다 복잡한 구조를 이해하게 됩니다. 파라메터의 갯수는 첫번째 레이어에서 3n + 3, 두번째 2 * 3 + 2, 세번째 2 * 1 +1 개가 됩니다.

이번에는 집가격 예측 모델에 예를 들어 보겠습니다. 사람이 모델링을 한다고 가정하면 방의 갯수, 크기는 가족의 크기와 관련이 있다고 생각할 것입니다. 그리고 우편번호는 이웃과 걸어다닐 만한 거리인지를 알 수 있을 것입니다. 그리고 우편번호와 부유한 정도를 통해 학교의 품질을 알수 있다고 생각할 것입니다. 이렇게 생각해낸 두번째 항목들 즉, 가족의 크기, 걸어다닐 수 있는 정도, 학교 품질이 집의 가격이 정해지는데 더 중요한 요소일 수 있습니다. 사람은 이렇게 컨택스트나 개념을 이용해서 모델링 할 수 있습니다. 그러나 Neural Network은 데이터 간에서 이러한 중요성과 관계를 스스로 학습하게 됩니다.

블랙박스 모델(black box model): 사람은 모델이서 어떤 것을 학습해서 다음 레이어에 전달하고 또 그것이 의미하는 것이 무엇인지 알 수 없기 때문에 딥러닝을 블랙박스 모델이라고 합니다.

엔드투엔드 러닝(end to end learning) : 보통 딥러닝은 입력과 출력을 정의하고 네트워크 모형을 정의한뒤에 데이터를 통해 훈련하는 방법입니다. 즉, 중간에 사람이 개입하여 어떤 작업을 하는 것이 없는 것 입니다. 이러한 방법을 end to end learning 이라고 합니다.  

어느 정도 숫자의 노드와 레이어를 만드는 것이 좋을까요?  정답은 없습니다. 두가지 팁을 드리면 첫째 아무도 모르기 때문에 해봐야 합니다. 훈련 데이터를 가지고 여러 개로 나누어서 여러 개의 다른 모델을 훈련해서 어떤 모델이 좋은지 알아보는 방법입니다. 두번째는 문제가 얼마나 복잡하냐에 따라서 달라집니다. 고양이 종을 분리하는게 어려울까요? 아니면 이미지가 밤인지 낮인지 분류하는게 어려울까요? 네...고양이 종을 분류하는게 더 어려울 것 같습니다. 따라서 고양이 종을 분리하는 모델을 만들때 보다 복잡한 많은 레이어와 노드가 있는 네트워크를 만들어야 할깝니다.

Optimizing

먼저 로스 함수를 정의 합니다.

Backward Propagation

Loss 함수를 편미분한 만큼씩 W와 B의 값을 수정해주는 것이 필요합니다. 이것을 모든 레이어 별로 실행해 줘야 합니다. 이때 시작하는 포인트가 Level 3 즉, w3 부터 미분해줍니다.  이렇게 하면 이후에 계산할 w2에서 앞서 계산한 값을 이용할 수 있기 때문에 계산이 쉬워집니다. 그래서 네트워크의 출력단 즉, 뒤에서 부터 계산하게 되는 것이지요.

이상으로 Neural Network에 대해서 알아보았습니다.

아래는 강의 링크 입니다.

https://www.youtube.com/watch?v=MfIjxPh6Pys&list=PLoROMvodv4rMiGQp3WXShtMGgzqpfVfbU&index=11