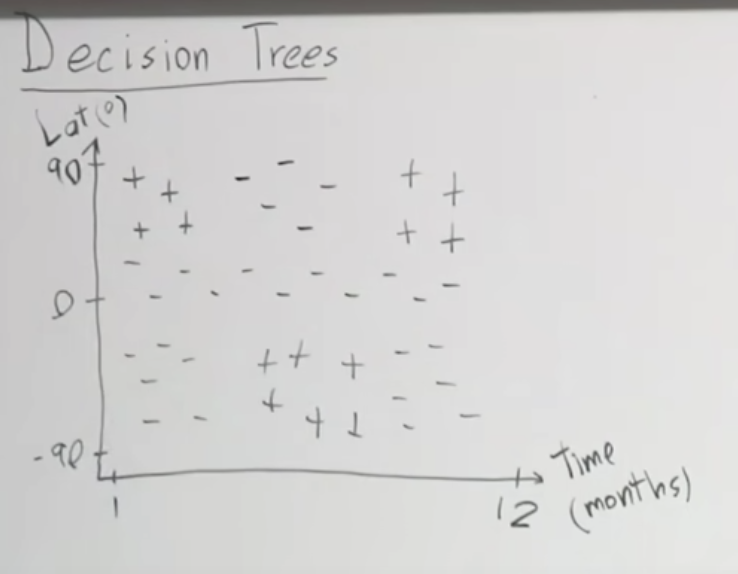
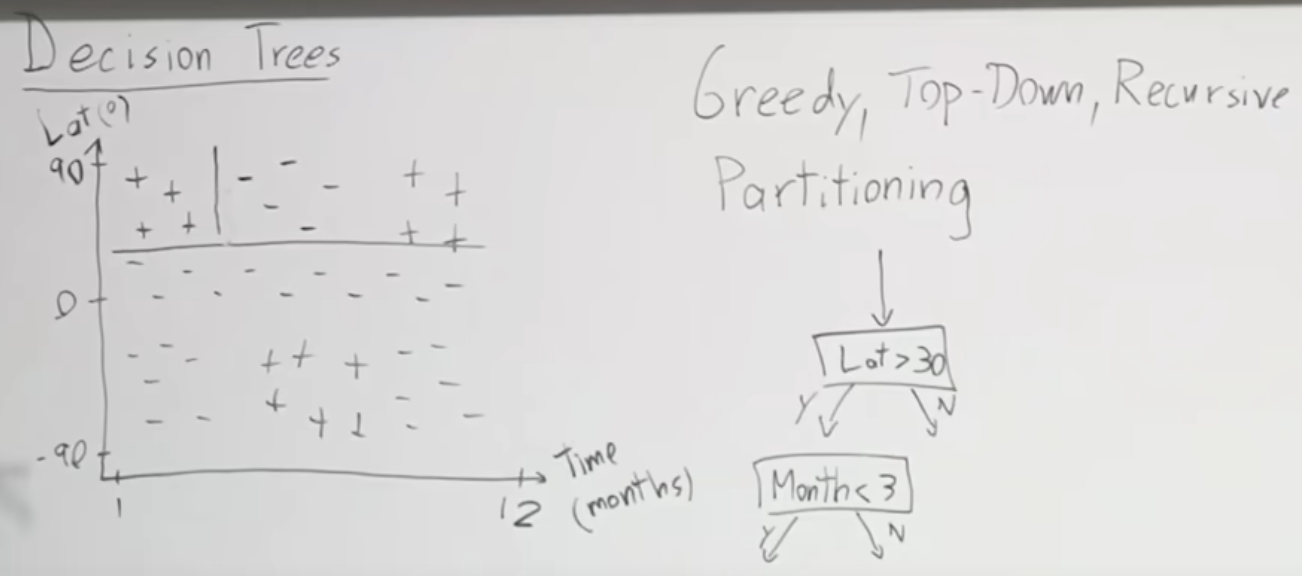
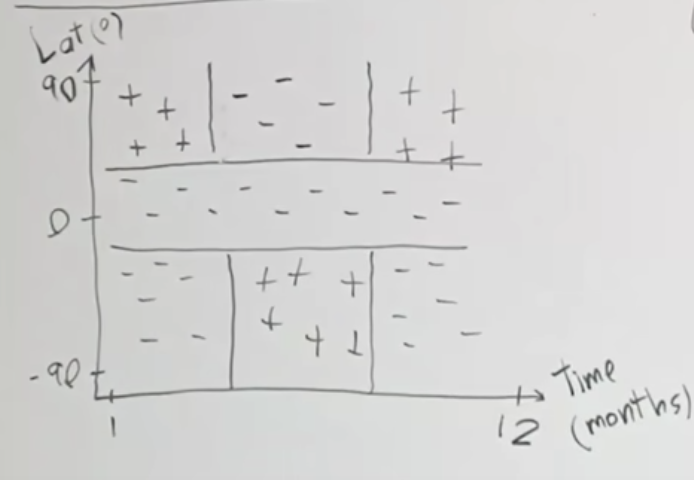
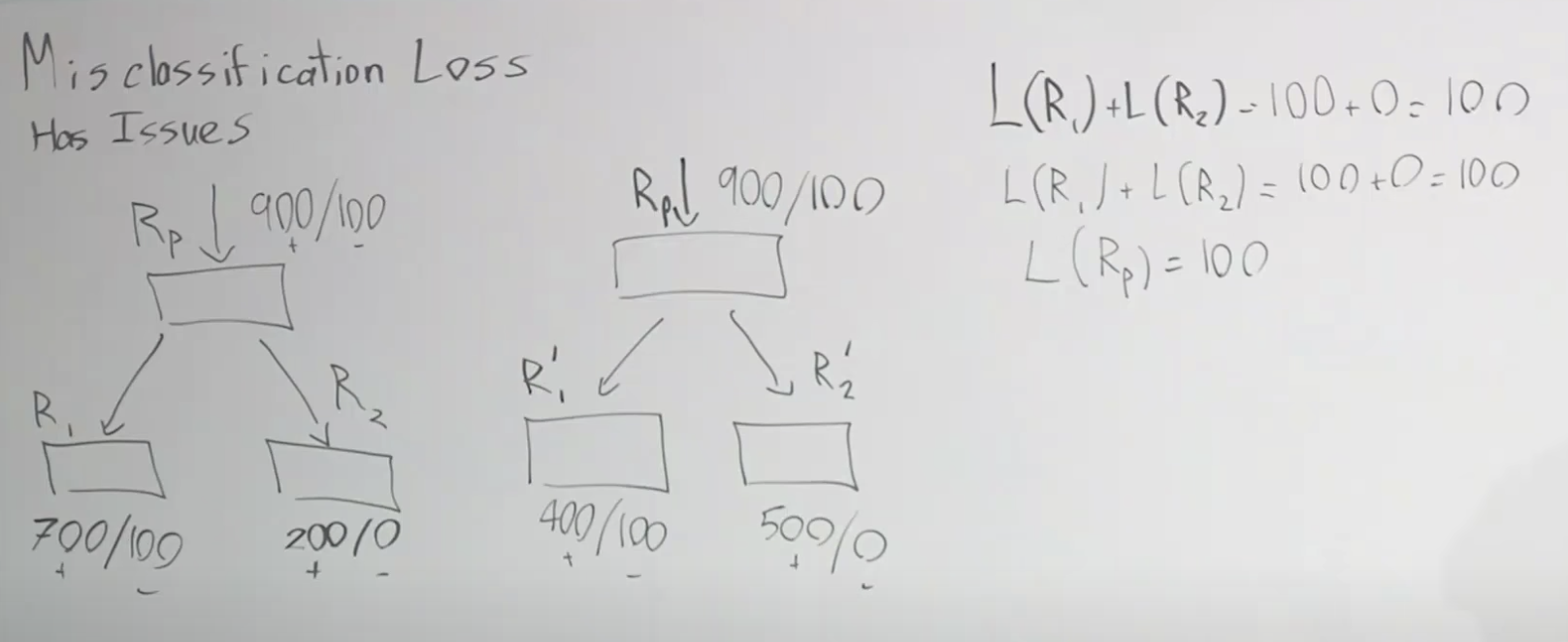
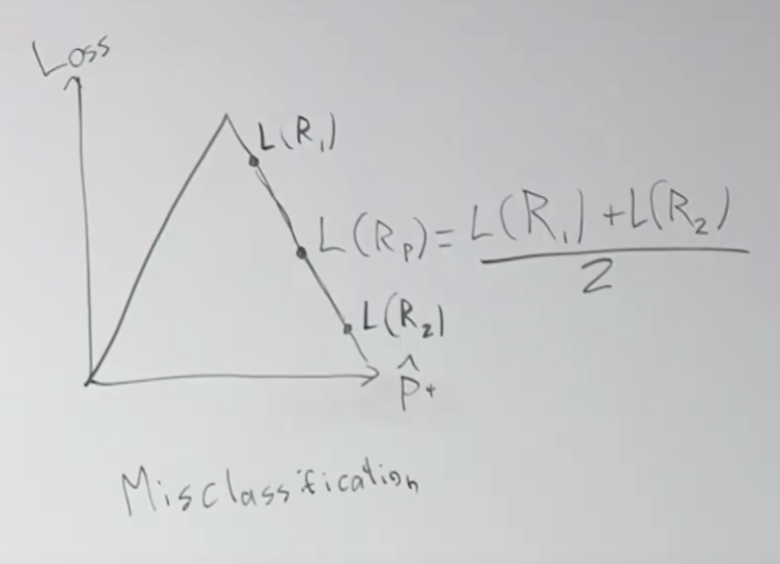
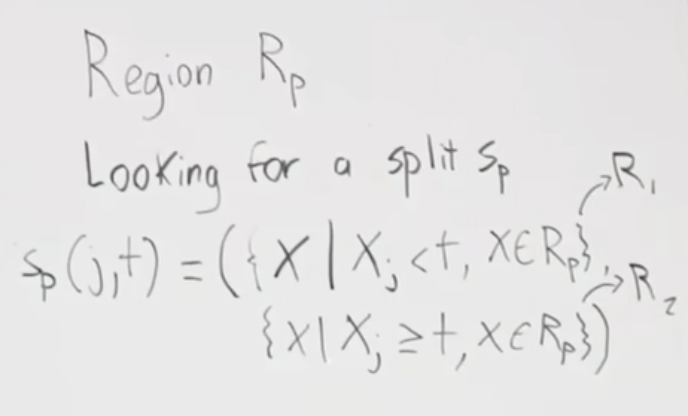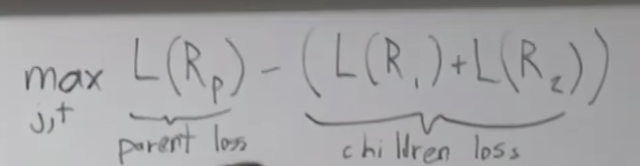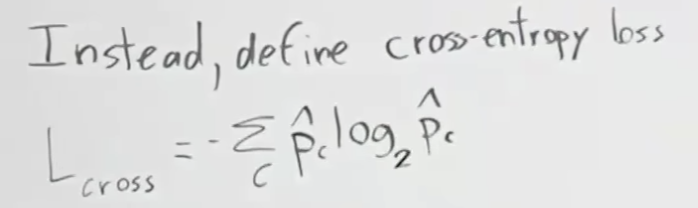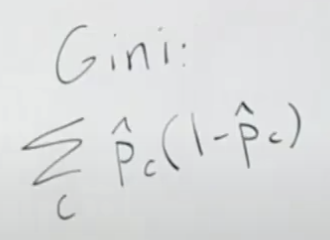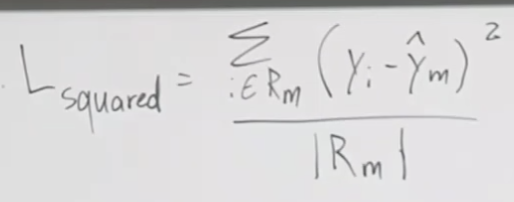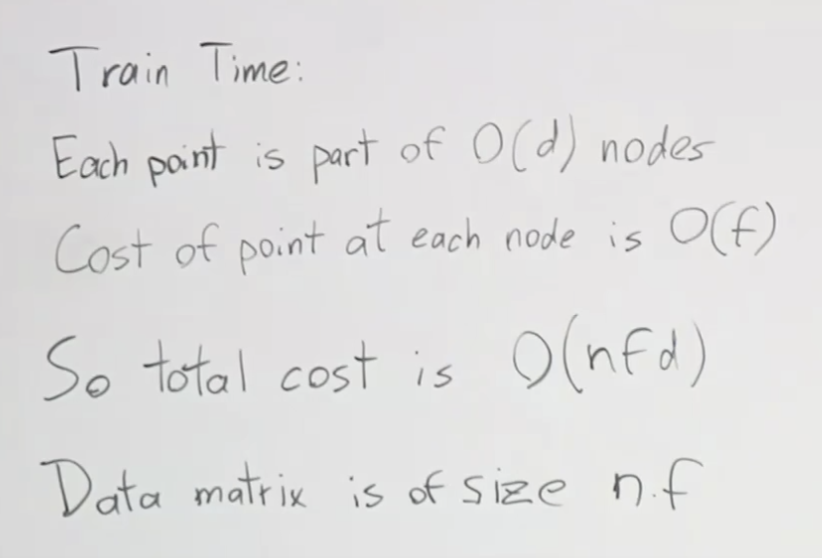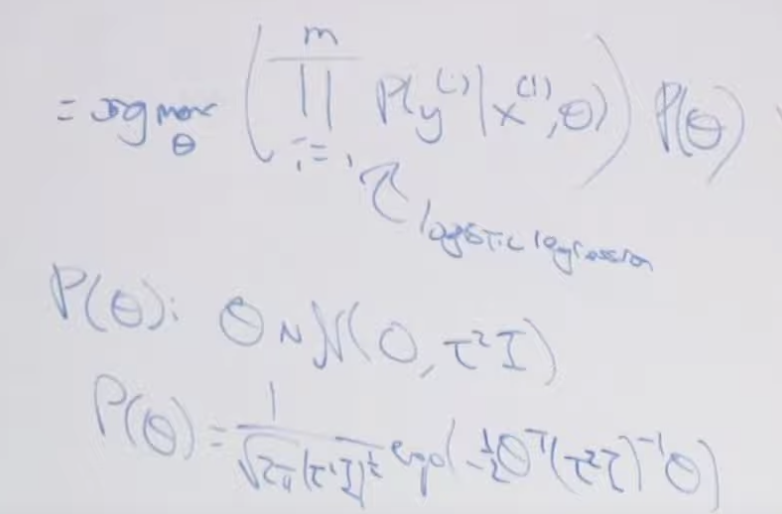주요 내용

• Deep Learning 이란
• Linear Regression 으로 본 신경망
• Neural Networks

Deep Learning  이란

딥러닝은 머신러닝의 한 분야로 특히 컴퓨터비전(CV), 자연어처리(NLP) 등에 많이 사용 되는 알고리즘 입니다. 새로운 처리 방법이지요.

딥러닝이 잘 동작하는 이유는 다음과 같습니다.

새로운 처리 능력의 향상: 첫번째 이유는 계산에 많은 비용이 드는 알고리즘 입니다. 많은 계산이 필요해서 병렬처리하는 것이 필요했는데 GPU가 사용 되었습니다. 많은 계산을 빠르게 처리할 수 있게된 것이지요. 

많은 데이터 : 인터넷 활성화에 따른 많은 데이터가 만들어 졌고 이렇게 많은 데이터를 가지고 모델을 만들 수 있게 되었습니다. 딥러닝 모델을 데이터가 다 많으면 많을 수록 더 잘 학습하게 됩니다.

새로운 알고리즘 : 많은 데이터와 새로운 계산 처리 기술을 이용하는 새로운 알고리즘을 만들어 냈습니다.

Logistic Regression 으로 본 신경망

첫번째 목표

지난 시간에 배운 로지스틱 리그리션을 활용해서 신경망을 설명해 보겠습니다. 첫번째 분류 문제로 고양이가 들어있는 이미지를 분류하는 것을 생각해 보겠습니다. 고양이가 있으면 1, 없으면 0을 나타내는 모델을 만들어 봅시다.  컴퓨터 공학에서 이미지를 3차원 행렬로 표현합니다. RGB 3가지 채널이 있기 때문이지요. 가로64픽셀, 세로 64픽셀의 칼라 이미지가 있다면, 가로 64픽셀 X 세로 64픽셀 X 3(RGB) 개의 픽셀 값으로 표현 됩니다. 이 값들을 하나의 벡터로 만들어서 입력 데이터로 사용합니다. 로지스틱 회귀에서의 공식을 적용해보면 아래와 같이 됩니다. 각 입력값 별로 가중치가 필요하니 64 * 64 * 3 개의 w가 필요합니다. 그래서 W의 크기가 (1, 12288)이 되었습니다.

모델을 훈련하는 절차는 다음과 같습니다. i) 먼저 w(가중치), 와 b(바이어스) 를 초기화 합니다.  ii) 최적의 w, b를 찾습니다. iii) 찾은 w,b 값을 이용해서 모델을 통해 예측을 실행 합니다. 두번째 단계가 특히 중요한데 여기서 로스(loss)와 Optimizer(Gradient descent) 같은 방법을 사용해서 최적의 w, b를 찾습니다. 로스는 MLE 를 이용해서 구하고 w와 b는 편미분한 값을 빼줌으로서 학습합니다.

여기에 사용되는 파라메터 갯수는 모두 몇개일 까요? 

바로 12,288개 + 1개 입니다. 즉, 웨이트 갯수와 바이어스 갯수의 합인 것이지요. 

두가지 기억하고 있어야 할 것이 있습니다. 첫째, 뉴런은 리니어 파트와 엑티베이션 파트로 구성된다는 것 입니다. 위의 그림에서 wx + b 부분이 리니어 파트이고 시그마 부분이 엑티베이션 파트 입니다. 동그라미가 바로 뉴런 입니다.  두번째, 모델은 아키텍처와 파라메터라는 것 입니다. 실무에서 모델을 만들어 배포했다는 것은 모델 아키텍처파일과 파라메터 파일을 배포했다는 것이고 이 두 파일을 이용해서 예측을 계산 / 실행하게 됩니다. 

두번째 목표

두번째 분류 문제를 생각해 보겠습니다.  이번에는 이미지에서 고양이, 사자 또는 이구아나를 찾는 문제 입니다. 어떻게 할 수 있을까요? 뉴런을 2개 더 만들어서 3개로 할 수 있겠습니다. 

그럼 이 모델에서는 몇개의 파라메타가 있을가요?  앞에서 소개한 파라메터 숫자의 3배가 필요합니다.  

그럼 어떤 데이터가 필요할까요?  네..이미지 데이터와 레이블 데이터 입니다. 이번 문제에서는 고양이, 사자, 이구아나 중에 어떤 동물인지를 표시해야하기 때문에 레이블 데이터가 필요합니다. 1번 이미지는 고양이 이고, 2번 이미지는 사자이고 등등...여기서 고양이, 사자 이런게 레이블 데이터 입니다. 즉, 레이블 데이터이란 훈련 데이터에 해당하는 정답 데이터를 말합니다. 이미지도 숫자로 입력되는 것처럼 출력도 고양이, 사자 이렇게 할 수 없어서 숫자나 위치를 정해야합니다. 이번 문제에서는 아래와 같이 레이블 데이터를 정하겠습니다. 하나의 이미지에 대해서 하나의 벡터 값으로 어떤 동물인지를 표시하는 것 입니다. 예를 들어 첫번째 값이 1이면 고양이를 표시하고, 두번째 값이 1이면 사자, 세번째 값이 1이면 이구아나를 의미합니다.

위와 같은 데이터를 가지고 모델을 훈련할 수 있습니다.  w, b를 초기화 시키고 로스를 계산하고 오차를 계산해서 w,b를 변경해 가면서 최적의 모델을 만들 수 있습니다.

이렇게 진행할 경우 그림 3에 제일 위에 있는 첫 번째 뉴런은 무엇을 배울까요?   바로 이미지에 고양이가 있는지 없는지를 학습하게 됩니다. 왜 그럴까요?  바로 아웃풋의 첫번째 위치가 바로 고양이의 존재 여부를 판단하는 내용이고 이 아웃풋이 첫번째 뉴런과 연결되어 있기 때문입니다. 아웃풋 벡터의 순서가 다른 것을 의미한다면, 즉 레이블 데이터가 바뀐다면 각 뉴런에서 학습하는 내용은 바뀌게됩니다.

그럼 이 모델은 여러 개의 동물이 있는 이미지에도 잘 분류할까요? 만약, 고양이와 사자가 들어있는 이미지를 모델에게 준다면 모델은 고양이도 잇고 사자도 있다고 판단할 것입니다. 아래 그림처럼 아웃풋 벡터에서 고양이와 사자에 해당하는 위치의 값이 1로 나올 것 입니다.

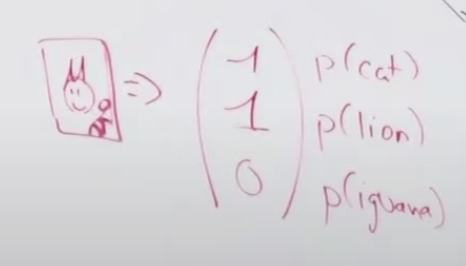
로스 계산은 아래와 같습니다. 각 동물별 로스의 합으로 전체 로스를 만듭니다.

세번째 목표

문제 3 세번째는 2번째 문제에서 처럼 두가지 동물을 모두 표시하는 것이 아니라 하나의 이미지에 가장 확실한 동물 한 종류만 표시하고 싶습니다. 어떻게 해야할 까요?  각 동물에 해당하는 출력 값들을 모아서 각 동물의 결과를 나누어 주면 됩니다. 그러면 각 동물별 결과치의 비율이 나오게 됩니다. 각 비율을 모두 합친 값은 1이 되겠지요. 에를 들면 처음 z1, z2, z3 값이 5, 3, 1 이었다면 소프트맥스 함수를 거쳐서 나온 값은 [0.86681333 0.11731043 0.01587624]이 됩니다. 결과 값이 z1이 제일 크네요. 이렇게 만드는 것이 소프트맥스(Softmax) 함수 입니다.  이러한 결과 값과 비교하기 위해 레이블 데이터는 고양이인 경우 [1,0,0], 사자인 경우 [0,1,0], 이구아나인 경우 [0,0,1] 로 등록되야 합니다. 이처럼 소프트맥스 함수를 통해 출력의 분포를 구할 수 있습니다.

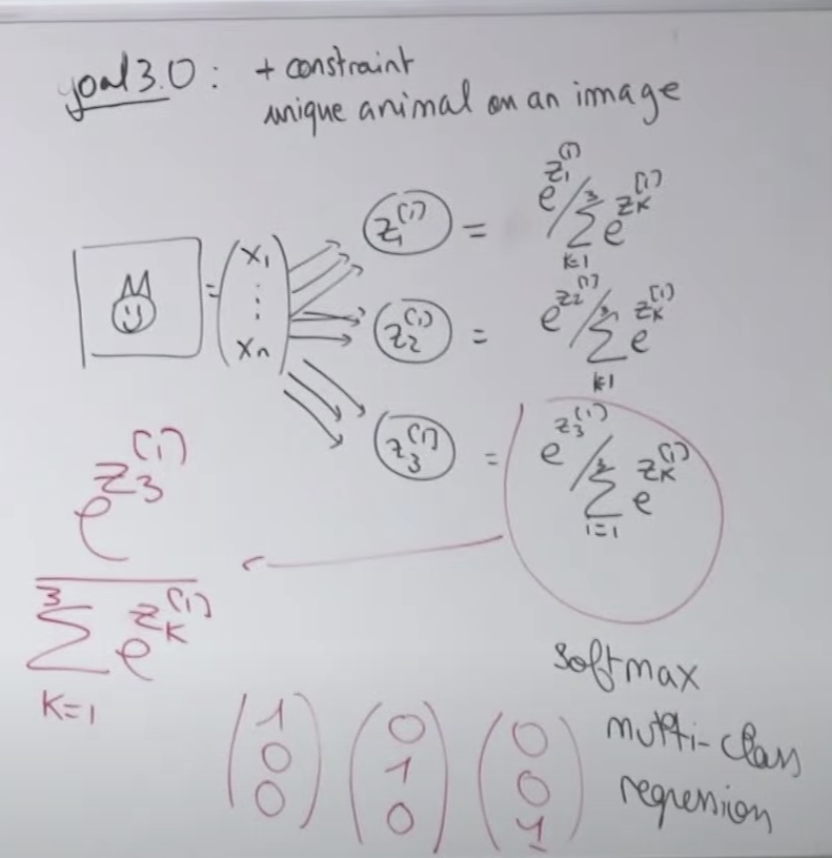
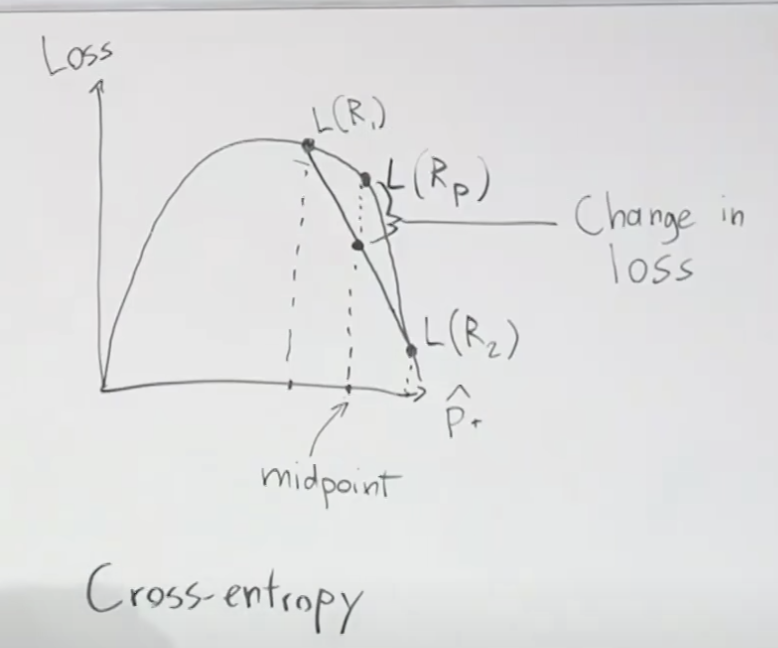
Softmax 함수 계산으로 출력값 z1, z2, z3사이에 서로 영향을 주기 때문에 로스는 크로스엔트로피로스(Cross Entropy Loss)를 이용합니다.

질문입니다. 만약 이미지에서 고양이의 존재를 있고 없고 판단하는게 아니라 고양이의 나이가 얼마가 되는지를 예측하는 문제라면 어떤 네트워크를 사용하시겠습니까?  문제 1을 풀기 위한 그림1 네트워크가 좋을까요?, 문제 2를 플기위한 그림3의 네트워크가 좋을 까요? 아니면 문제 3을 풀기위한 그림5의 네트워크가 좋을까요? 네 문제 3을 풀기위한 그림5 네트워크를 연령대 구분으로 나누어서 사용할 수 있을 것 같습니다. 첫번째는 10대, 두번째는 20대...이런 식으로요...물론 하나의 출력 노드를 가지는 리그레션 모델로 만들 수도 있습니다. 리그레션 모델로 한다면 시그모이드 함수를 사용하지 말아야 겠지요. 그 대신 신경망에서 많이 사용하는 레루 ReLU 함수를 이용하는 것이 좋습니다. 로스함수는 L1 놈/노름( |y^ - y|) 또는 L2 놈/노름(||y^ - y||L^2)를 사용하면 되겠습니다.

Neural Networks

다시 이미지에 고양이가 있는지 없는지를 구분하는 첫번째 문제를 생각해 보겠습니다. 로지스틱 회귀의 신경망 버전에서와 달리 중간에 히든 레이어를 추가할 수 있습니다. 이것은 입력과 출력에서 보이지 않는 신경망 계층을 의미합니다. 신경망의 첫번째 레이어는 단수한 엣지 같은 것을 식별해내고 두번째 레이어에서는 귀나 입 같이 좀더 복잡한 모양을 찾아냅니다. 이처럼 신경망의 깊이가 깊어질 수록 보다 복잡한 구조를 이해하게 됩니다. 파라메터의 갯수는 첫번째 레이어에서 3n + 3, 두번째 2 * 3 + 2, 세번째 2 * 1 +1 개가 됩니다.

이번에는 집가격 예측 모델에 예를 들어 보겠습니다. 사람이 모델링을 한다고 가정하면 방의 갯수, 크기는 가족의 크기와 관련이 있다고 생각할 것입니다. 그리고 우편번호는 이웃과 걸어다닐 만한 거리인지를 알 수 있을 것입니다. 그리고 우편번호와 부유한 정도를 통해 학교의 품질을 알수 있다고 생각할 것입니다. 이렇게 생각해낸 두번째 항목들 즉, 가족의 크기, 걸어다닐 수 있는 정도, 학교 품질이 집의 가격이 정해지는데 더 중요한 요소일 수 있습니다. 사람은 이렇게 컨택스트나 개념을 이용해서 모델링 할 수 있습니다. 그러나 Neural Network은 데이터 간에서 이러한 중요성과 관계를 스스로 학습하게 됩니다.

블랙박스 모델(black box model): 사람은 모델이서 어떤 것을 학습해서 다음 레이어에 전달하고 또 그것이 의미하는 것이 무엇인지 알 수 없기 때문에 딥러닝을 블랙박스 모델이라고 합니다.

엔드투엔드 러닝(end to end learning) : 보통 딥러닝은 입력과 출력을 정의하고 네트워크 모형을 정의한뒤에 데이터를 통해 훈련하는 방법입니다. 즉, 중간에 사람이 개입하여 어떤 작업을 하는 것이 없는 것 입니다. 이러한 방법을 end to end learning 이라고 합니다.  

어느 정도 숫자의 노드와 레이어를 만드는 것이 좋을까요?  정답은 없습니다. 두가지 팁을 드리면 첫째 아무도 모르기 때문에 해봐야 합니다. 훈련 데이터를 가지고 여러 개로 나누어서 여러 개의 다른 모델을 훈련해서 어떤 모델이 좋은지 알아보는 방법입니다. 두번째는 문제가 얼마나 복잡하냐에 따라서 달라집니다. 고양이 종을 분리하는게 어려울까요? 아니면 이미지가 밤인지 낮인지 분류하는게 어려울까요? 네...고양이 종을 분류하는게 더 어려울 것 같습니다. 따라서 고양이 종을 분리하는 모델을 만들때 보다 복잡한 많은 레이어와 노드가 있는 네트워크를 만들어야 할깝니다.

Optimizing

먼저 로스 함수를 정의 합니다.

Backward Propagation

Loss 함수를 편미분한 만큼씩 W와 B의 값을 수정해주는 것이 필요합니다. 이것을 모든 레이어 별로 실행해 줘야 합니다. 이때 시작하는 포인트가 Level 3 즉, w3 부터 미분해줍니다.  이렇게 하면 이후에 계산할 w2에서 앞서 계산한 값을 이용할 수 있기 때문에 계산이 쉬워집니다. 그래서 네트워크의 출력단 즉, 뒤에서 부터 계산하게 되는 것이지요.

이상으로 Neural Network에 대해서 알아보았습니다.

아래는 강의 링크 입니다.

https://www.youtube.com/watch?v=MfIjxPh6Pys&list=PLoROMvodv4rMiGQp3WXShtMGgzqpfVfbU&index=11 

Lecture 10 - Decision Trees and Ensemble Methods | Stanford CS229: Machine Learning (Autumn 2018)

주요 내용

• Decision trees 의사결정 나무
• Ensemble Methods 앙상블 방법
• Bagging 배깅
• Random Forests 랜덤 포레스트
• Boosting 부스팅

Decision Trees 의사결정 나무

시간(월)과 위도를 가지고 스키를 타기 좋은지 아닌지를 구분하는 분류기를 만든다고 생각해 봅시다. 데이터를 통해 가능한 지역과 시간에 +를 표시하고 불가능한 지역과 시간에 -를 표시하면 아래와 같습니다.

Greedy top-down recursive partitioning
모든 케이스들을 측정한다는 측면에서 Greedy하다고 할 수 있고, 전체 데이터를 가지고 분류해나가기 때문에 top-down 이라고 말할 수 있습니다. 그리고 데이터를 분류하고 나서 분류된 한 부분을 가지고 다시 분류하기 때문에 recursive 하다고 말할 수 있습니다.
첫번째는 위도가 30도 인지를 가지고 분류할 수 있습니다. 그래서 위도가 30보다 큰 지역과 작은 지역으로 나누어 집니다. 이어서 두번째로는 시간(월)을 가지고 분류할 수 있습니다. 3월보다 작은 달인지 아니닌지로 구분합니다. 이렇게 나누어진 그림이 아래와 같습니다.

이러한 방법으로 계속 분류를 하면 아래와 같이 분류할 수 있습니다.

아래는 p(positive, +) 지역(Region Rp)을 찾는 것을 함수 Sp로 만들었을때의 공식입니다. 입력 변수로 j는 피처를 나타내고 t는 임계값을 의미합니다. Rp는 Region parent 즉, 상위/부모의 지역을 말합니다. 아래 공식을 설명해보면 j 에 해당하는 Xj 값이 임계값 t 보다 작을 때는 첫번째 지역 R1에 할당하고, 크거나 같을 경우 두번째 지역 R2에 할당합니다.

그럼 분류 후 얼마나 틀렸는지를 계산하는 로스는 어떻게 계산할 까요?

그런데 잘못 분류한 로스 계산에 문제가 있습니다. 아래 두 그림에서 처럼 실제로 다르게 분류를 했음에도 불구하고 로스는 오른쪽에 보이듯이 좌우 모두 100 입니다. 심지어 부모 노드의 로스 L(Rp)도 100으로 같습니다.

그래서, 이런 문제를 해결하기 위해 단순 로스가 아닌 크로스 엔트로피 로스(Cross-entropy loss)를 사용하게 됩니다.

크로스 엔트로피 로스는 L(R1)과 L(R2)의 평균에 해당하는 지점에서 곡선과 직각이되는 점-L(Rp)와의 차이(Gain)를 계산하는 것 입니다. 아래에서 Change in loss로 적혀 있는 부분이 Gain입니다. 즉, 부모 노드에서 발생한 로스 보다 자식 노드 2개에서 발생한 로스의 평균이 더 적게 되는 경우 입니다.

이것은 Gini 값이라고 해서 아래와 같이 정의된 값도 많이 쓰입니다.

아래는 잘 못 분류된 경우를 설명하는 그림입니다. 부모 노드의 로스(L(Rp))가 결국 자식 노드 2개의 평균과 같은 것이 되버리기 때문에 자식 도드에서는 의미 없는 분류를 한 것과 같습니다.

Regression Trees
이번에는 Regression Trees에 대해서 알아보도록 하겠습니다. Decision Trees의 예로 사용했던 스키 예를 이용하겠습니다. 다만 적합한지 아닌지 + - 로 구분했던 것을 적설량으로 구분하는 예를 들어보겠습니다. Decision Tree에서와 같이 위도와 시간 월에 따른 위치에 적설량을 숫자로 표시합니다. 그리고 이것을 잘 분류하게 됬을 경우 아래처럼 구분하는 선들이 그려지게 됩니다.

지역 Rm에 해당하는 예측값 y^m을 수식으로 나타내면 아래와 같습니다. 이것은 지역 Rm에 있는 모든 수의 합을 숫자 갯수로 나누어서 계산하는 값으로 결국 지역의 평균 값이 됩니다.

로스는 스퀘어드는 MSE(Mean Squared Error)와 같이 각 예측 값에서 평균값(y^m)을 뺀값의 제곱을 누적하여 전체 갯수로 나누어서 구합니다.

Categorical Vars 를 가지고도 모델을 만들 수 있습니다. 그러나 9개의 카테고리가 있다고 만 가정해도 2^9만큼의 분리가능한 것들이 생겨서 너무 복잡하고 비효율적입니다.

왼쪽에 North, Equator, South로 카테고리를 분류 할 수 있습니다. 이는 특히 이진트리(Binary trees)의 경우도 적용할 수 있습니다. 각 분류의 갯수 별로 소팅한뒤에 숫자에 따라 분류해 나갈 수 잇습니다.

Regularization of Decisioon Trees
트리 모델을 모든 훈련데이터에 훈련 시키면 결국 모든 훈련케이스를 만족시키는 트리를 만들게 되어 결국 최종 결과가 하나씩 연결되는 Overfitting이 발생하게됩니다. 이를 방지하기위해 정규화가 필요한데 여기에 사용되는 다양한 휴리스틱 정규화 방법에 대해서 알아보면 아래와 같습니다. 최소 리프 사이즈를 제한 하거나, 트리의 깊이를 제한 하거나, 노드들의 최대 수를 정해 놓거나, 최소로 줄어드는 로스를 정해 놓거나, 검증 데이터에서 잘못 분류된 가지를 제거하는 등이 있습니다. 특히, min decrease in loss의 경우 부모노드 보다 자식노드가 최소 어느정도는 더 분류를 잘해야 하는 지를 정하는 방법으로, 데이터 피처의 중요도-잘 분류하는 데이터 피처에 따라서 위에서 아래로 정리되게 만드는 방법입니다.

Runtime
n은 예제수, f는 피처수, d를 나무의 깊이라고 하면, 테스트 시간은 O(d)가 되고 이때 깊이 d는 log2n 보다 작습니다. 여기서 log2n이 의미하는 것은 말 그대로 훈련 예제수에 로그를 취한 값 입니다. 다시 말하면 전체 예제수로 훈련해서 만들어진 훈련된 트리를 이용해서 테스트를 하게 되기 때문에 훈련에서 만들어진 트리의 깊이에 따라 속도가 달라지게되고 이 깊이는 훈련을 통해 잘 분리되도록 하는 이진트리(하위노드가 2개인 트리)를 만들었다고 할경우 결국 훈련데이터의 예제수에 로그를 취한 값이 보다 작아지게 됩니다. 리프 노드에 하나의 예제가 달린다고 최학의 경우를 가정한 것이 log2n입니다. 아무튼 너무 당연한 이야기 인데요 트리의 예측 속도는 트리의 깊이 만큼 비교해야하기 때문에 O(d)입니다.

그럼 훈련 시간은 어떻게 될까요? 각 포인트는 O(n) 속도의 노드에 속한 한 부분이고, 각 노드에서 포인트의 비용은 O(f)입니다. 이 말은 피처 f가 위도, 시간-월 이렇게 2개있을 경우 O(2) 만큼의 시간이 걸린다는 말입니다. 깊이 마다, 각 노드에서 피처마다 처리하는 시간이 필요하고 이런 계산을 예제수 만큼해야하니 모두 곱한 O(nfd)가 훈련 시간이 됩니다.

Downsides
이제 의사결정트리의 단점을 알아볼까요? 선형회귀로 간단히 분류가 가능한 +와 - 데이터 들이 있습니다. 그런데 이것을 의사결정나무 Decision Trees로 분류하게 되면 많은 분류 기준이 필요하여 복잡한 트리가 만들어 질 수 있습니다. 속도도 느려지고 잘 분류가 안되는 경우도 생길 수 있습니다.

요약- 장점/단점
의사결정나무의 장점과 단점은 아래와 같습니다. 장점으로는 먼저 설명하기 쉽습니다. 모르는 사람에게도 예를 들면 10개 질문을 통해서 분류한다고 설명할 수 있습니다. 모델을 해석하기 쉽고, 범주형 변수(Categorical Vars)에 유용하며, 속도가 빠릅니다. 단점으로는 분산이 큰 모델로 훈련 데이터에 오버피팅 되기 쉽습니다. 변수 사이에 상호작용이 작은 경우에 분석에 약하고(반대로 상호작용이 큰 경우에는 강합니다), 그리고 예측 정확도가 낮습니다.

Ensemble Methods 앙상블 방법

여기서 독립 가정을 제거하면 전체 모집단의 평균(X-bar)에 대한 분산은 아래와 같이 계산할 수 있습니다. 공식을 풀어서 이해해 보면 p 에 의해 연관된 x 샘플이 많을 수록 분산은 커지고 데이터수(n) 이 클수록 분산이 작아지게 됩니다.

이처럼 정확도를 높이기 위한 방법중 하나가 앙상블 ensemble이며 앙상블에는 다양한 방법이 있습니다.
다른 알고리즘을 쓸수 있고, 다른 훈련 데이터 셋을 사용할 수도 있습니다. 베깅과 부스팅이라는 기법도 있습니다. 베깅의 대표적인 예는 랜덤포레스트이고 부스팅의 대표적인 예는 에이다부스트(Adaboost)와 xGboost 입니다.

Bagging 배깅

베깅에 대해서 알아보면 다음과 같습니다. 배깅은 부트스트랩 에그리게이션(Bootstrap Aggregation)의 축약어 입니다. 실제 모집단 P에서 샘플 S를 뽑아서 훈련 셋을 사용합니다. 이때 우리는 샘플이 모집단과 같다고 가정하고 모델을 만듭니다. 여기에 부트스트랩이라는 기술을 추가하는데 이것은 샘플에서 다시 샘플을 추출하여 Z라는 샘플을 만들고 이것을 훈련에 이용하는 것을 말합니다.

이렇게 생성된 여러 개의 샘플 z를 가지고 모델 G를 여러번 훈련할 수 있고 그 결과를 평균할 수 있습니다. 이 부분이 바로 에그리게이션 Aggregation 파트에 해당하는 내용입니다. 즉, 여러 샘플 데이터 셋을 가지고 훈련한 모델의 여러 결과들을 합치는 부분입니다.

이 기술을 적용하면 바이어스와 베리언스(오차와 분산, Bias-Variance)에 변화를 주게 됩니다. 앞서 분산에 대한 공식을 정리한 것이 있는데 이것을 부스팅에 적용하면 아래와 같습니다. 즉, Var(x-)의 내용중 분모를 M (샘플z 수)로 바꾸어 준것 밖에 없습니다. 부스팅을 적용하면 공식에 있는 p를 줄입니다. 그리고 데이터가 많을 수록 분산을 줄입니다. 반면 오차는 살짝 올라 갈 수 있습니다.

의사결정트리는 높은 분산에 낮은 바이어스를 가지고 있기 때문에 배깅과 매우 잘 맞습니다. 배깅이 분산을 낮추어 주기 때문입니다.

Random Forests 랜덤 포레스트

Boosting 부스팅

부스팅은 배깅과 다르게 바이어스를 줄이는 효과가 있습니다. 변수 사이의 상효작용에 강합니다. 이 기술은 반복적인 모델 훈련을 합니다. x1, x2 피처를 가지고 분류 모델을 만든 다고 가정해 보시죠. 아래 왼쪽과 같이 분류모델을 만들어 분류를 할 수 있는데 빨간색 박스 처럼 오분류하는 경우가 발생합니다. 이러한 경우 다음 훈련에서 해당 예제 샘플의 가중치를 높혀서 훈련하면 오른쪽의 그림처럼 큰 +와 -를 만들수 있고 이들을 고려한 분류모델을 만들면 그림과 같이 위/아래로 나누는 분류선(모델)을 만들 수 있습니다. 이런 식으로 반복해 나가면서 모델을 학습하는 방법이 부스팅 입니다.

아래는 강의 링크 입니다.
https://www.youtube.com/watch?v=wr9gUr-eWdA&list=PLoROMvodv4rMiGQp3WXShtMGgzqpfVfbU&index=10

Lecture 9 - Approx/Estimation Error & ERM | Stanford CS229: Machine Learning (Autumn 2018)

주요내용

• Setup/ Assumptions
• Bias Variance Trade-off
• Approx/Estimation Error 
• ERM: Empirical Risk Minimizer
• Uniform Convergence
• VC Dimensions

Setup/ Assumptions

모델을 개발하는데 기본적인 가정사항에 대해서 알아봅시다. 

1. Data Distribution D.    (x, y) ~ D (Train, Test)

데이터는 특정 분포(D)를 가지고 훈련 데이터와 테스트 데이터는 동일한 분포 (D)로 나온다는 가정입니다. 

2. Independent Samples

데이터들은 특정분포를 갖지만 어떤 값이 들어올지는 모르는 랜덤 변수이고 이를 학습 알고리즘(Estimator)에서 받아서 학습된 추정치인 h^ 또는 θ^을 만들어 냅니다.

Bias Variance 

Data view에서 바라본 Bias / Variance는 지난 시간에 봤던 것과 같이 아래 그림과 같습니다. 3개의 모델이 있다고 가정한 것이고 Underfit, Just Right, Overfit 된 모델을 선으로 그린 그림입니다.

파라메타 관점에서 바라본 Bias/Variance는 아래 그림과 같습니다. 왼쪽 그래프 A, C는 낮은 Variance를 가지고 있으며(점들이 모여있습니다.), 오른쪽의 B, D는 높은 Variance를 가지고 있습니다(점들이 왼쪽보다 퍼져있습니다). 위의 A, B 그래프는 높은 Bias를 가지고 있으며(중앙의 별과 점들의 중앙이 멀리 있습니다.), 아래 C, D는 낮은 Bias를 가지고 있습니다(별과 점들의 중앙이 가까이 있습니다). 가운데 별은 정답(영역) 입니다. 그래프의 점들은 한번 훈련이 됬을때의 θ1, θ2의 값에 의해 그려진 것입니다. 

훈련 데이터의 양이 많아지면 점들의 간격이 줄어듭니다. Variance 가 작아집니다.

다시 말하면 훈련 데이터 수(m)가 무한대로 많아 진다면 Variance[θ^]이 0에 가까워 집니다. 그리고 훈련 데이터가 많아지면 추정값인 θ^(세타헷)이 실제값인 θ*(세타스타)에 가까워 집니다.  모든 데이터를 가지고 훈련해서 θ^을 통해 추정하면 θ*와 같은 값이 됩니다. (이론적으로 그렇다는 것이고 실제로 모든 데이터를 훈련할 수 없는게 현실이고 그리고 가능하다고 해서 그말은 모델을 만들 필요가 없다는 의미 없습니다. 그래서 위에서 말한 것처럼 같은 값으로 가까워진다는 표현이 더 좋은 것 같습니다.)

Fighting Variance

그래서 Variance를 줄이는 방법에는 여러가지가 있습니다. 먼저 훈련 데이터수를 늘리는 것입니다. 두번째는 정규화(Regularization)를 하는 것입니다. 그래서 점들을 모이게 만드는 것입니다. 

Approx/Estimation Error 

가설공간에 제일 가능한 가설(g)과 제일 좋은 가설들의 집합(h*), 데이터로부터 학습된 가설/파라메타(h^) 을 표시하면 아래와 같습니다. 여러번 훈련해서 여러개의 h^이 나올 수 있고 이것을 묶은 것이 H(타원) 입니다.  그래서 학습된 파라메타(h^)와 정답(g: ground truth) 의 차이 인 에러가 발생하게됩니다. ℇ(h)는 Risk error / Generalization error(정규에러)라고 불립니다. 하나의 파라메타 샘플(s)에 대한 에러 ℇ^s(h) 는 Empirical Risk로 불립니다. 이 것은 아래와 같이 모든 h(xi)와 yi가 틀린 경우 확률을 평균한 것 입니다. 리우며 이것은 데이터 x 값이 주어졌을 때 의 에러를 말합니다. 

ℇ(g) 는 Bayes Error 또는 제거가 불가능한 에러(Irreducible Error)라고 불립니다. 훈련데이터에서 다른 x 값에 같은 y 값을 갖는 경우가 그예입니다.  Approximation Error, Estimation Error, Irreducible Error 등을 알수 있습니다.

가설 공간에 에러를 표시해 보면 아래와 같습니다.

Fighting Bias

바이어스를 줄이는 방법은 H를 크게 / 넓게 만드는 것입니다. 또는 아예 다른 알고리즘을 사용하는 것도 좋은 시도가 될 수 있겠습니다.

ERM: Empirical Risk Minimizer

ERM은 러닝 알고리즘 중 하나 입니다.

Uniform Convergence 균등 수렴

(1)번은 모집단의 h를 가지고 예측에러와 실제에러를 비교하는 방법이고, (2)번은  모델의 h^을 통해 발생한 에러와 모집단의 정답 h*을 이용했을때의 에러를 비교하는 것입니다.    위의 (1),(2) 번을 각각 비교하기 위해 다음 이미지에 있는 툴 1,2를 이용합니다.

두번째 툴은 Hoeffding's Idea 입니다.

이것을 그래프로 그려보면 아래와 같습니다. 하나의 셈플로 에러를 측정한 임피리컬 에러(파란색 점선)와 정규화된 에러(E(h)) ( 검정색 실선)을 볼 수 있고, hi라는 특정 샘플(hi)에서 두선의 에러 차이를 보면 아래와 같이 표시될 수 있습니다.  ​이러한 임피리컬 에러들을 정규화 에러선으로 변환시키는 방법중 하나가 Uniform Convergence 균등수렴 방법입니다. 

균등수렴과 Hoeffding 방법을 이용하면 아래와 같이 전체 가설에 대해서 공식을 만들 수 있습니다.

이러한 공식을 사용하는 방법은 아래와 같이 2가지를 고정하고 다른 값을 찾는 방법입니다. 두 변수를 0보다 크다고 가정하고 m 사이즈를 구했네요.

위 그래프를 공식으로 표시해 보면 아래와 같습니다.(중간부터 아래쪽)

​

VC(Vapnic-Chervonenkis) Dimension​

​​

Lecture 8 - Data Splits, Models & Cross-Validation | Stanford CS229: Machine Learning (Autumn 2018)

주요내용

• Bias/ Variance
• Regularization 정규화
• Train/dev/test splits
• Model selection & Cross validation

Bias/ Variance

이전 강의에서 예를 들었던 주택 사이즈별 가격 데이터를 가지고 이야기 해 보겠습니다. 같은 데이터를 가지고 아래와 같이 3가지의 모델을 만들 수 있습니다. 왼쪽은 언더피팅(underfit)된 1차원 모델의 High bias 그래프이고 가운데는 적당한 2차원 모델, 오른쪽에는 다중 선형모델로 오버피팅(Overfitting)된 모델의 High Variance 그래프 입니다.

Regularization 정규화

아래는 로지스틱 회귀 공식 입니다. - 부호 뒤의 람다|| ||^2가 Regularization 내용입니다. 이 변수를 통해 곡선의 구부러진 정도를 조정할 수 있습니다.

λ람다에 따른 곡선의 변화를 보면 아래와 같습니다. λ가 아주크면 0에 가까워지는 군요.

SVM의 경우 수많은 변수를 세타함수를 통해서 만들어 사용하는 데(고차원 매핑) 왜 오버피팅이 되지 않을 까요? 그것은 - λ||θ||^2 와 같은 역할을 하는 것이 SVM에서는 minimize ||w||^2 때문에 결국 같은 효과 즉 오버피팅을 막는 효과가 있습니다.

나이브 베이즈의 예를 들어 보겠습니다. 전 시간에 예를든 스팸 분류기도 좋고 트위터 데이터에 대한 감성분석도 좋습니다. 이러한 분류 문제를 다룬다고 할때 특히 이렇게 피처는 많고(10,000) 예제 데이터는 적을때(100)는 로지스틱 회귀에 정규화 Normalization 을 추가하여 개발한 모델의 성능이 나이브 베이즈 보다 좋습니다. 정규화를 이용하지 않으면 오버피팅되기 때문에 성능이 좋지 않습니다.   보통은 피처가 예제 데이터 보다 10배이상 크면 정규화를 이용합니다.

정리하면 

Frequentist와 Bayesian 학자들 사이의 차이점에 대해서 설명합니다. Frquentist는 MLE를 구하고 베이지안 학자는 MAP(Maximization A Posteriori)를 구합니다.

y축은 에러율, x 축은 모델의 복잡도를 기준으로 그래프를 그려보면 아래와 같습니다.  일반적인 그래프는 모델 복잡도가 낮으면 언더핏되고 모델 복잡도가 높아질 수록 점점 에러가 줄어들게 됩니다. 그러다가 중간이 지나면 다시 에러율이 상승하는데 이렇게 상승된 상태의 모델을 오버피팅된 모델이라고 합니다.  곡선이 위로 꺽기기 시작하는 중간지점이 가장 좋은 모델 복잡도를 가진(에러가 가장 낮은) 모델입니다.

여기에 정규화(Normalization)을 위해 λ를 사용할 경우 λ크기에 따라 에러의 변화를 만들 수 있습니다. λ가 너무 크면 제일 왼쪽 처럼 언더피팅되고 λ를 0으로 설정하면 (정규화를 안하면) 오른쪽 처럼 오버피팅됩니다. 적당한 λ값을 설정해주면 중간에 가장 에러가 낮을때를 만들 수 있습니다.

Train/dev/test splits

일반적으로 트레인/개발/테스트로 나눕니다. 트레인/검증/테스트(Train/Validation/Test) 로도 불립니다. 10,000 개의 example 데이터가 있을 경우 모델의 복잡도를 하나씩 높여가면서 결과를 보고, 또는 람다 값 등 변수들을 조정하면서, 그리고 정규화를 적용해 보면서 모델을 만듭니다.

이때 데이터셋(S)를 train용 dev용, test용 으로 분리합니다. dev 는 development를 말합니다.

각각의 모델을 S(train) 테레인 데이터를 가지고 훈련하여 적당한 하이퍼파라메타를 찾습니다.  

옵션으로 논문 페이퍼를 위한 내용 필요시 테스트 데이터를 가지고 사용합니다. 이전에는 한번도 사용되지 않은 데이터 입니다.

degree를 높여가면서 S(dev)개발용 데이터를 이용한 에러가 아래 왼쪽처럼 감소하다가 증가하는 degree가 나옵니다. 보기에는 4.9에러가 나온 degree의 모델을 사용하면 될 것 같은데 자세히 보면 그전, 그리고 전전 에러율이 5.0, 5.1로 큰 차이가 없습니다. 이러한 경우에 실제 모델 degree의 차이때문에 생긴 에러 차이가 아니라 바이어스나 모델의 다른 변수에 의한 것일 수 있습니다. S(test)로 측정해서 선택하도록 합니다.

예전에는 대부분 데이터 셋(S)은 아래처럼 70%와 30%로 나누거나 60%, 20%, 20%로 나누었습니다.  그런데 예제 데이터가 10,000,000개 있을 경우 6:2:2로 분리하는 것이 좋을까요? 정말 test 데이터가 2,000,000개 필요한지 생각해 봐야합니다. 온라인 추천이라든가 매우 작은 소수점아래 자리까지 고려하는 경우에는 많은 test 데이터가 필요합니다. 그러나 다른 업무에서는 이렇게 많이 필요하지 않을 수 있습니다. 데이터가 충분히 많이 있다면 90%:5%:5%로 나누는 것이 좋습니다. 그리고 여기에 원하는 정확도의 차이(0.01%까지 고려해야하는지 0.0001%까지 고려해야하는지) 에 따라서 dev/test 수를 조정하면 됩니다.

Model selection & Cross validation

이처럼 데이터를 트레인/데브/테스트로 분리하는 것을 (Simple) Hold-out cross validation 이라고 합니다. 그리고 dev set은 Cross Validation Set 이라고도 불립니다.

그럼 데이터 셋이 작은 경우에는 어떻게 할까요?  예를 들면 m=100 개 셈플이 있다면 70개를 훈련에 30개를 개발(검증)에 써야합니다. 훈련과 검증에 너무 작은 수 입니다. 

이러한 경우 K-fold Cross Validation을 이용합니다. k는 임의 의 숫자인데 통상적으로 10을 씁니다. 여기서는 설명을 위해 5로 합니다. 전체 데이터셋(S)를 K로 나눈 숫자만큼의 덩어리로 만들어서 , k번 반복하는 동안 한번에 한 덩어리 데이터를 가지고 훈련하는 방법입니다. K 번 훈련해서 나온 에러를 평균해서 하나의 degree(복잡도, 하이퍼 파라메터)에서의 에러율을 구합니다. 이런 절차를 degree 숫자만큼 반복하면서 진행하면 어느 degree에서 가장 작은 에러가 발생하는 지 알수있습니다. (측, 최적의 degree모델을 찾을 수 있습니다.) 데이터를 가지고 1번의 훈련과 검증이 가능 했던 것을 k 번 반복할 수 있게되어서 훈련을 더 잘할 수 있습니다. 알고리즘은 아래의 오른쪽에 나와있습니다.

옵션으로 해도되고 안해도 되는데, 이렇게 해서 선택하게된 degree의 모델을 가지고 전체 100% 훈련데이터를 가지고 훈련해서 모델을 만들 수 있습니다.

이러한 Cross Validation 은 특히 적은 데이터를 가지고 있을때 유용합니다.

Leave-one-out Cross Validation

훈련 데이터의 개수가 아주 적을 때(100보다 같거나 작을 경우) Leave-one-out Cross Validation을 쓰면 좋습니다.  예를 들어 훈련 데이터가 20개(m=20)일 경우의 예를 들면 데이터들을 아주 작게 즉 1개 단위로 사용할 수 있게 분리해서 사용 하는 방법입니다. 즉, 20개로 분리하고 19개를 훈련에 사용하고 1개로 검증하고, 전에 사용했던 훈련 데이터중 하나를 검증으로 사용하고 나머지를 모두 훈련데이터로 사용하는 방법입니다. 이렇게 하면 모델의 훈련과 검증을 20번 할 수 있습니다. 컴퓨팅에 많은 비용이 소모되므로 데이터가 많을 경우는 사용하지 않습니다. 말씀 드린 대로 100개 이하인 경우만 사용을 권장합니다.  

Feature Selection

피처 선택(Feature Selection)은 여러 개의 피처 중에서 성능에 많은 영향을 미치는 피처들을 찾는 것을 말합니다. 전방 피처 선택(Forward Feature Selection)과 후방 피처 선택(Backward Feature Selection) 방법이 있습니다. 전방 피처 선택의 예를 들면 5개의 피처가 있다고 가정할 때 가장 영향력이 큰 피처를 하나씩 추가해 가는 방법입니다. 아래의 경우 x2가 제일 중요한 피처라고 발견된 경우 x2는 고정하고 추가로 x2와 x1, x2와 x3, x2와 x4, x2와 x5 처럼 x2피처에 하나의 피처를 추가할 경우 어떤 피처가 가장 영향력이 큰지를 찾는 방법입니다.  이러한 방법으로 하나씩 피처를 선택해나가는 방법이 전방 피처 선택법(Forward Feature Selection)입니다.