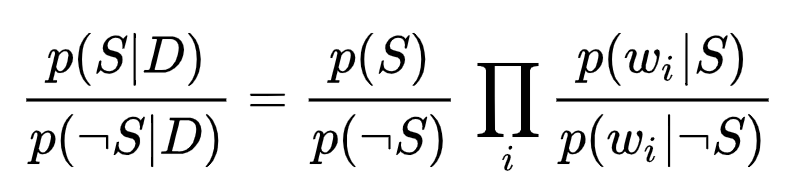The Yellow Lion King 데이터와 함께 살아가기

가능도/우도/Likelihood

위키피디아

통계학에서, 가능도(可能度, 영어: likelihood) 또는 우도(尤度)는 확률 분포의 모수가, 어떤 확률변수의 표집값과 일관되는 정도를 나타내는 값이다. 구체적으로, 주어진 표집값에 대한 모수의 가능도는 이 모수를 따르는 분포가 주어진 관측값에 대하여 부여하는 확률이다. 가능도 함수는 확률 분포가 아니며, 합하여 1이 되지 않을 수 있다.

정의

확률변수 X 가 모수 θ 에 대한 확률분포 Pθ(X)를 가지며,  X가 특정한 값  x로 표집되었을 경우, θ의 가능도 함수 L(θ |x) 는 다음과 같이 정의된다.

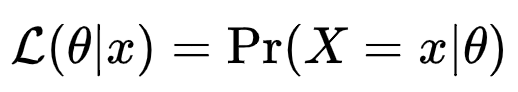
예 2

동전을 던져서, 앞면(H)이 나오는 확률을p_H 라고 하자. 이때, 앞면이 두번 나오는 확률은 p_H^2이다.
만약 p_H=0.5 일 경우, 두번 모두 앞면이 나올 확률은 0.25이다:
P(HH | p_H=0.5)=0.25
이를 통해, 관측결과가 HH 라면, p_H=0.5 의 가능도는 0.25라고 말할 수 있다.
L(p_H=0.5|  HH)=P(HH | p_H=0.5)=0.25
그러나 이것은 관측결과가 HH라면, p_H=0.5 의 확률은 0.25 이라고 말하는 것과 같지 않다.
이를 위해서는 베이지안 추론의 개념이 필요하다. 특히, 베이 즈 정리 (Bayes 's theorem)는 사후 확률 (밀도)이 가능도 (likelihood)과 사전 확률에 비례함을 말한다.

개요

확률은 관측값(x)를 입력해서 얻은 값입니다. x가 발생할 가능성을 표시한 것이 확률입니다. Pr(x)로 표시합니다. 그런데 위에서 표시된 가능도의 공식에서 가능도는 Pr(X=x|θ) 로 되어있습니다. Pr, X, θ라는 조건이 더/다르게 들어있습니다.  즉, 확률과는 다르게 θ까지 추가로 고려한 확률을 가능도라 부릅니다. 여기서 θ는 모수의 확률분포를 계산하는 데 사용되는 변수 입니다. 아주 간단히 말하면 가능도는 관측치(x)와 확률함수의 변수(θ)를 가지고 계산된 값입니다. 확률함수는 확률밀도함수 또는 확률질량함수를 말합니다. 연속 확률 분포에서는 확률계산을 위해 확률밀도함수(PDF)를 쓰고 이산 확률 분포에서는 확률질량함수(PMF)를 씁니다. 아래에서 예를 들어보겠습니다.

Example

이산 확률분포(이항분포) : 동전 던지기 예시 

이항분포이기 때문에 확률질량함수를 사용합니다.

이항 분포 확률질량함수(PMF) 는 아래와 같습니다.

우리는 이미 동전을 던질때 앞면(H)/뒷면이 나올 확률이 0.5라는 것을 알고 있습니다. 즉, p가 0.5인 것을 알고 있습니다. 그래서 앞면이 두번 나올 확률을 계산하면 다음과 같습니다.

P(H) = 0.5라고 할때, P(HH) = P(H) * P(H) = 0.5 * 0.5 = 0.25

그럼 가능도는 얼마일까요? 공식은 L(θ|x) 입니다.  확률질량함수는 위에서 정의된 것을 이용하면되고 그 안의 (θ)변수 p 를 0.5로 입력해서 계산하면 아래와 같습니다.

L(θ|x) = Pr(X=x|θ) =  Pr(X=HH|0.5) = (2, 2)* 0.5^2 * (1-0.5)^(2-2) = 0.5 * 0.5 = 0.25

확률 값과 가능도 값이 같네요. 이말을 풀어서 설명하면

(확률로 설명) 동전을 던져서 앞면이 나올 확률이 0.5인 동전을 두번 던져서 앞면이 두번 나올 확률은 0.25이고,

(가능도로 설명) 동전을 던져서 앞면이 나올 확률(θ)이 0.5인 경우 동전을 두번 던져서 앞면이 두번 나올 가능성이 0.25이다. 다른 점은 확률(θ)를 입력 변수로 사용한다는 것입니다. 그럼 앞면이 나올 확률값을 0.4를 바꾸어서 계산해 보겠습니다.

(n, k)p^k (1-p)^(n-k)

= 0.4^2 = 0.16

이 결과는 앞면이 나올 확률값이 0.4인 동전을 두번 던져서 앞면이 두번 나올 가능성은 0.16이다.라는 의미입니다. 이번에는 0.8로 바꾸어서 계산해 보겠습니다.

0.8^2 = 0.64

이 결과는 앞서 설명한 내용과 유사합니다.  앞면이 나올 확률값이 0.8인 동전을 두번 던져서 앞면이 두번 나올 가능성은 0.64 이다. 라는 말입니다. 생각해보시지요. 동전이 두 종류가 있습니다. 하나는 앞면이 나올 확률이 0.4이고 다른 하나는 앞면이 나올 확률이 0.8입니다.  둘중에 어떤 동전을 선택했는지는 모르지만 둘중 하나의 동전을 선택해서 던진다고 가정할 때 두번 모두 앞면이 나올 가능성을 계산할 수 있습니다. 0.4 동전을 던지면 가능성이 0.16이고 0.8인 동전을 두번 던지면 0.64 가능성이 있습니다. 이처럼 동전의 앞면 확률(사전확률)이 얼마인지 모를때 가능도를 계산해서 어느 동전일 가능성이 높은 지(사전확률을)를 계산해서 찾을 수 있습니다. 이경우 가장 가능성이 높은 동전의 앞면확률을 찾으면 당연히 1인 동전이 되겠지요.(왜냐하면 1일때 가능도가 1(100%)가 되니까요.) 이처럼 최대 가능도를 찾을 수 있는데 이를 최대가능도법(MLE)라고 합니다.  

정규분포 : 키 측정 예시

이번에는 정규분포의 설명을 위해 한사람의 키를 가지고 설명해 보겠습니다.

정규분포함수 확률밀도함수(PDF)

= f(x) = 1 / σ√2π * e^(-1/2 * ((x-u)/σ)^2)

정규분포의 확률을 계산하려면 확률밀도 함수를 사용합니다. 이를 이용하려면 확률밀도함수 공식에 있는 모평균(u), 즉 실제 키를 알아야하 합니다. 다른 말로 설명하면 실제 키를 알야야 확률을 구할 수 있습니다. 이 말은 실제키가 170일때 측정값 169가 나올 확률이 얼마인지를 계산할 수 있다는 말입니다. 표준편차(σ)는 1이라고 가정하고 위의 공식에 대입해 보겠습니다.

f(x) = 1 / σ√2π * e^(-1/2 * ((x-u)/σ)^2)
= 1 / √2π * e^(-1/2 * (169-170)^2)
= 1 / √2π * e^(-1/2 * 1)
= 1 / 2.5066 * e^(-1/2)
= 1 / 2.5066 * 0.6065 
= 0.2419

정규분포의 가능도를 계산해보겠습니다.

똑 같은 가정, 즉, 실제 키가 170이고 표준편차가 1이라면 확률값과 가능도는 일치합니다. 그러나 실제 키와 표준편차를 모를 때는 확률을 구할 수 없습니다. 그대신 가능도를 구합니다. 왜냐하면 가능도는 169가 평균이 170일때 나올 가능도를 알려줍니다. 그럼 다시 평균이 169일때 나올 가능도를 구해보겠습니다.

f(x) = 1 / σ√2π * e^(-1/2 * ((x-u)/σ)^2)
= 1 / √2π * e^(-1/2 * (169-169)^2)
= 1 / √2π * e^(-1/2 * 0)
= 1 / √2π * e^(0)
= 1 / 2.5066 * 1
= 0.3989 * 1
= 0.3989

키 169는 평균이 170인 집단에서 뽑힐 가능도가 0.2419이고 평균이 169인 집단에서 뽈힐 가능도가 0.3989 로 169인 집단의 가능도가 더 큽니다. 상식적으로도 이해가 됩니다. 평균이 제일 많이 발생하는 숫자일 가능성이 높으니까 평균이 170일때 보다는 (같은 값인) 169일때 더 뽑힐 가능성이 높습니다.

이해가 되시나요?! ^^

Summary

지금까지 가능도에 대한 정의와 실제 예를 들어 그 값을 계산해 보았습니다. 

다시 정리하면 가능도는 관측치(x)와 확률함수의 변수(θ)를 가지고 계산된 값입니다. 이 계산 방법은 분포마다 다릅니다.

정규분포의 확률을 구하려면 실제 집단의 평균(모평균)을 알아야 하는데 대부분이 모르는 경우이기 때문에 계산할 수 없고, 이런 변수들을 추정값으로 이용하여 가능도를 구할 수 있습니다.

의문이 듭니다. 가능도는 가정한 변수를 통해 얻은 값이라 정확하지도 않을 것 같은데 이러한 가능도는 어디에 어떻게 쓸수 있을까요?

위에서 잠깐 언급한 것처럼 최대 가능도를 갖는 변수(theta)를 구하는데 사용될 수 있습니다. 관측된 여러 값들과 추정되는 모수를 가지고 가능도를 구할 수 있는데 추정값들을 바꾸어가면서 가장 가능도가 높은 모수를 구할 수 있습니다. 이렇게 되면 모수(모평균, 모분산)등을 몰라도 가능도가 가장 놓은 모수를 구할 수 있습니다. 즉, 모르고 있던 실제 값들을 가장 높은 가능도로 알 수 있게 됩니다. 이러한 방법이 최대가능도법(MLE)입니다.

다음에는 최대가능도법(MLE)과 그 활용방법을 알아보겠습니다.

https://bigdatamaster.tistory.com/158

추가: 아래에 있는 위키의 예제를 보시면 이해가 되실껍니다. (설명이 조금 딱딱하긴 하네요) ^^

예 2

동전을 던져서, 앞면(H)이 나오는 확률을p_H 라고 하자. 이때, 앞면이 두번 나오는 확률은 p_H^2이다.
만약 p_H=0.5 일 경우, 두번 모두 앞면이 나올 확률은 0.25이다:
P(HH | p_H=0.5)=0.25
이를 통해, 관측결과가 HH 라면, p_H=0.5 의 가능도는 0.25라고 말할 수 있다.
L(p_H=0.5|  HH)=P(HH | p_H=0.5)=0.25
그러나 이것은 관측결과가 HH라면, p_H=0.5 의 확률은 0.25 이라고 말하는 것과 같지 않다.
이를 위해서는 베이지안 추론의 개념이 필요하다. 특히, 베이 즈 정리 (Bayes 's theorem)는 사후 확률 (밀도)이 가능도 (likelihood)과 사전 확률에 비례함을 말한다.

주요 내용

• PDF가 무엇인가?
• 자세히 알아보기
• PDF 해보기

 

PDF가 무엇인가?  

PDF 확률 밀도 함수를 위키피디아에서는 아래와 같이 정의하고 있습니다.

확률론에서 확률 밀도 함수(確率密度函數, 영어: probability density function 약자 pdf)는 확률 변수의 분포를 나타내는 함수로, 확률 밀도 함수  f(x)와 구간 [a,b] 에 대해서 확률 변수  X가 구간에 포함될 확률 P(a <= X <= b) 는

 

가 된다.

확률 밀도 함수 f(x)는 다음의 두 조건을 만족해야 한다.

1. 모든 실수값 x에 대해 f(x) >= 0}

확률 밀도 함수와 누적 분포 함수에는 다음과 같은 수식이 성립한다.

'연속 사건에서 x가 주어 졌을 때의 확률을 구하는 함수'

자세히 알아보기

PDF란 연속 사건(데이터)을 입력받아서 이것이 발생할 확률로 바꾸어 주는 함수를 말합니다.

시그마 σ : 표준편차,  x : 관측값,  뮤u : 모평균(모집단의 평균)

참고로 독립/이산 확률의 경우 확률질량함수(PMF: Probability Mass Function)로 확률을 계산 할 수 있습니다. 아래는 위키피디아에 정의된 내용입니다.
확률 질량 함수(確率質量函數, probability mass function, PMF)는 이산 확률 변수에서 특정 값에 대한 확률을 나타내는 함수이다. 이 함수는 연속 확률 변수에서의 확률 밀도 함수와 대응된다.
예를 들어, 주사위를 한 번 굴릴 때의 값을 나타내는 확률 변수가 X일 때, 이 확률 변수에 대응되는 확률 질량 함수는  fX(x)=1/6 이다.

한번 생각해 보시지요.  PDF가 왜 필요할까요? 설명을 못하시겠다면 다시 처음부터 다시 한번 읽어보시지요.(이해 안되는 부분이나 이상한 부분은 댓글 남겨주시면 답변 드리겠습니다.)

PDF 해보기

관측값(키) = 168, 169, 170, 171, 172

이 값을 가지고 각각의 키가 측정될 확률을 구하면 어떻게 될까요?  한번 추정해 보시지요 과연 어떤 관측값의 확률이 가장 높을 까요?

평균 = (168 + 169 + 170 + 171 + 172) / 5 = 850 / 5 = 170
(원래 u는 모평균인데 여기서는 측정치의 평균을 구했습니다.)

분산 = 차이값 제곱의 평균 = 루트[ (값 - 평균)^2 / n ] 
= 루트 [ (168 - 170)^2+(169 - 170)^2+(170 - 170)^2+(171 - 170)^2+(172 - 170)^2 / 5 
= 루트 [ (-2^2 + -1^2 + 0^2 + 1^2 * 2^2) / 5 ]
= 루트 [ (4 + 1 + 0 + 1 + 4) / 5 ]
= 루트 [10 / 5]= 루트 [2] = 1.414

표준편차 σ = 루트(분산) = 루트(1.414) = 1.189

Naive Bayers Classification 나이브 베이지안 분류에는 크게 3가지로 가우시안, 다항분포, 베르누이(이항분포)가 있다.
이중에서 분류의 목적과 데이터 유형에 따라서 사용할 방법을 선택할 수 있다.
이번에는 다항분포 나이브 베이지안 분류에 대해서 알아보자.
비연속적인 데이터 값에 대해서 여러가지의 분류중에서 선택/분류하는 방법이다.
가장 많이 알려진 예시가 바로 스팸 메일 분류다. 즉, 메일의 제목과 내용을 보고 이 메일이 스팸 메일일지 아니면 정상적인 메일일지를 분류하는 알고리즘에 사용할 수 있다. 이러한 방법은 기계학습 방법중에서 지도학습(Supervised Learning)에 해당한다.
한번 생각해보자. 아래의 내용은 메일에 들어있는 내용을 단어로 표시한 것이다. 1번과 2번의 메일 중 어느 것이 스팸 메일 일까?

1번: 광고 출시 기념 할인 대상 선물 대박 핸드폰 
2번: 회의 사장 회사 오전 대표님 연락 메일 예약 출시

당신은 몇번을 선택했나? 왜 그렇게 선택했나?
내 생각에는 1번이 스팸 메일 일 꺼라고 선택했는데, 이유는 1번에 나오는 단어들이 스팸 메일에서 자주 보이는 단어이기 때문이다.
이처럼 각 단어가 스팸 메일에서 나타나는 확률을 계산하고 모든 단어의 확률을 더해서 하나의 메일이 스팸 확률을 계산하는 방법이 바로 다항분포 베이지안 분류 방법이다.


다항분포 나이브 베이지안 알고리즘의 공식을 이해하기 쉽게 풀어서 상세하게 설명하겠다.
(아래 위키 페이지의 내용을 기반으로 설명)

먼저 간단한 공식 읽는 방법을 이해해 보자

p 는 확률을 말하고, w는 단어, i는 순서를 표시하고, C는 클래스를 말한다. 즉 풀어서 말하면 C라는 클래스에서 단어 wi가 나타날 확률이다. 실제 계산하는 방법은, 모든 C클래스에 속하는 단어의 출현 횟수 중에서 wi가 얼마나 나타났는지 계산하면 된다.(짧게 말하면, C클래스에 나타난 wi 출현 건수 / C클래스에 나타난 모든 단어 출현수 = wi 가 C클래스라는 조건에서 나타날 확률)
예를 들면, p(광고 | 스팸메일) 의 의미는
스팸메일이라는 클래스 조건에서 광고라는 단어가 나올 확률을 말한다.

그래서 우리는 C 클래스가 주어졌을때 D라는 문서가 나타날 확률을 아래와 같이 공식으로 만들 수 있다.

이 공식[공식2]을 풀어서 설명하면
C클래스(스팸메일)에 대하여 D(메일)이 속할 확률은 = C클래스(스팸메일)라는 조건에서 D의 각 단어(wi)가 나타날 확률을 모두 구하고 이 확률 들을 누적곱한 것
이다.
이처럼 [공식2]를 말하는 이유는 계산 할 수 있는 값 이기 때문이다. 즉, 스팸메일로 분류된 메일들의 내용을 통해서 스팸메일에 할당된 문서들의 워드 별로 스팸 메일에서의 출현 확률을 계산해 낼 수 있기 때문이다.

그런데 우리가 원하는 확률 값은 (새로운 메일 문서)D가 주어졌을때 C(스팸)일 확률이다.
수식으로는

이다

[공식2] 에서와 같이 만들 수 있지만 문제는 D라는 조건에서의 C클래스에 모든 단어가 출현할 확률을 계산할 수 없다. 왜냐하면 우리는 어떤 D가 들어올지 모르기 때문이다. 모든 단어 조합에 해당하는 D를 만들면 해당 문서가 C클래스에 속할 확률을 알 수 있겠지만 모든 단어 조합의 문서를 만든다는 말은 결국 무한대에 가깝기 때문에 만들 수 없다.
그런데 다행히도 우리는 아래의 조건부 확률 공식을 이용해서 공식을 바꿀 수 있다.

[공식4]를 이용하여 [공식3]을 아래와 같이 바꿀 수 있다.

이와 같은 방법으로 반대도 알 수 있다.

[공식6]을 이용해서 공식 5의 오른 쪽 분자에 있는 p(D ∩ C)를 p(C) p(D|C) 로 아래와 같이 바꿀 수 있다.

우리는 이공식을 공식2에 의해서 아래와 같이 바꿀 수 있다.

그런데 우리는 아직도 p(D)를 계산할 수가 없고
이렇게 계산해서 나온다고해도 그냥 클래스에 속할 확률인 값만 나온다. 예를 들면, 스팸 메일일 확률 88.833%, 일반 메일일 확률 88.799%. 이렇게 나와서 판단 하기 어렵다.
그래서 간단하게 스펨과 일반 두가지의 클래스만 있다고 가정하고 위 공식의 C를 스팸(S)과 일반(-S)로 바꾸면 아래와 같다.

결국 스팸 가능성이 더 큰지, 아니면 일반일 가능성이 더 큰지를 비교하면 되므로 계산해서 나온 두 값을 비율로 만들어서 어느 것이 더 높은지 판단 할 수 있다. 이를 위해 위의 공식 2개를 비율로 만들면 아래와 같다. 같은 항의 값으로 나눈 것이다.

이것을 조금 더 보기 좋게 정리하면 아래와 같다.

이렇게 계산하면 두 클래스간의 유서도비(우도비)율이 나오는데, 문제는 클래스에 속한 단어의 숫자가 일치하지 않고 발생 차이가 많이 날 수 있기 때문에 (예: 스팸단어 1,000개, 일반단어 100,000개) 로그를 취해서 크기/스케일을 맞추어 준다.

이렇게 해서 나온 값이 크면 스팸일 가능성이 높은 것이고 낮으면 일반 메일일 가능성이 높은 것이다. 이러한 구분/분류를 위해 테스트 데이터를 통해 적당한 기준값(Threshold)을 설정해 준다.

자, 이론도 알았으니 다음에는 이러한 나이브 베이지안 알고리즘을 이용하여 분류기를 직접 만들어 보자.