Perceptron
퍼셉트론이 중요한 이유는 분류 문제를 다루는 알고리즘 중에서 기본적이고 역사적으로 의미가 있는 알고리즘이기 때문입니다. 너무 간단하고 한계가 많아서 실제로 많이 사용되지는 않지만 이것이 기반이되어 최근에 많이 쓰이는 딥러닝이 발전되었기 때문에 퍼셉트론을 이해하는 것은 매우 중요하다고 할 수 있습니다.
자 설명을 시작해 보았습니다.
위키의 정의는 아래와 같습니다.
퍼셉트론은 이진 분류를 위한 지도학습 알고리즘 중 하나이다. 이진 분류기는 숫자로 된 벡터를 인풋이 어떤 특정 분류 그룹에 속하는지를 판단할 수 있는 함수이다. 이것은 선형 분류기 중 하나이다. 다시 말하면, 피처 벡터와 가중치의 조합을 통해 선형 예측함수를 기반으로 예측을 만들 수 있는 분류 알고리즘을 말한다.
In machine learning, the perceptron is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class.[1] It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector.
쉽게 풀어서 설명해 보겠습니다.
퍼셉트론은 아주 간단히 말하면 '알고리즘' 입니다. 조금 더 길게 설명하면 '분류 알고리즘'입니다. 더 길게 설명하면 '여러 데이터 항목의 입력을 받아서 출력은 이진으로 0또는 1을 출력하는 분류 알고리즘' 입니다. 이렇게 하기 위해서 분류 선(모델라인)을 만듭니다.
이 내용은 아래와 같이 정의 할 수 있습니다.
g(z) = { 1 : z >= 0, 0 : z < 0 }
이 공식을 풀어서 설명하면 입력 z가 0 과 같거나 더 크면 1, 0보다 작으면 0을 출력하는 함수 입니다.
이것이 퍼셉트론 알고리즘 입니다.

이러한 구조에서 w를 조정하면 다양한 논리 연산자(AND, OR, NOT) 로직을 입력값에 적용하여 출력값을 얻을 수 있습니다. x1, x2, x3는 입력값이고 0또는 1의 값을 갖습니다. w1, w2, w3는 각 입력값에 대한 가중치 값입니다. y는 출력값, 즉 0 또는 1입니다. 이때 가중치 w를 조정하면 다양한 로직의 결과로 y 값을 만들어 낼 수 있습니다. 예를 들면, x1을 키, x2를 몸무게, x3를 허리둘래 값이라고 하고 우리가 찾고자 하는 것은 비만 여부(1: 비만, 0: 정상)를 출력하는 모델을 만들 수 있습니다. 이때 가중치 w를 각각 다르게 설정함으로서 키, 몸무게, 허리둘래가 출력값 y, 비만 여부에 미치는 영향도를 조정할 수 있습니다.(+-모두) 이를 위해 y를 가장 잘 맞추는 w들을 찾으면 좋은 모델을 만든 것이라고 할 수 있습니다. 그래서 w는 학습을 하면서 계속 바꾸어가면서 좋은 값인지 아닌지를 확인하는 과정을 거칩니다.
아래는 조금 더 복잡하지만 자세하게 정리된 내용입니다.

X는 입력값을 행렬로 표시했고, x0 = 1 은 바이어스 입니다. 자연스럽게 발생하는 오차를 보정하기 위해 사용한다고 생각하시면 좋겠습니다. 아웃풋을 z로 표시했고 이러한 z값을 만들기위해 함수(h(w^T x))를 이용합니다. x는 자연수(integer), w는 실수(float), z는 논리값(boolean)입니다.
처리는 앞서 설명한 간단한 그림의 내용과 같습니다. 입력 받은 x1, x2,...xD를 가중치 w와 곱해서 모두 더한 값을 아웃풋으로 출력하는 내용입니다. 이러한 계산은 아래와 같이 2단계의 절차를 거칩니다.

왜 두단계로 나누어 졌을 까요? 앞에서 설명한 내용은 첫번째 단계에서 하는 내용 같은데 두번째 단계에서는 무엇을 하는 것일까요? 왜 필요할까요?
Activation Function
존재의 이유를 찾는 방법중하나는 그 존재가 없으면 어떻게 되는 지 생각해 보는 것입니다. 그래서 첫번째 단계만 계산하고 출력해보겠습니다 x0 =1, x1 = 1, x2= 1, w0 = 0, w1 = 0.5, w2 = 1 이라고 가정 하겠습니다. 이를 활용해서 첫번째 단계를 계산해보면
a = x0 * w0 + x1 * w1 + x2 * w2 = 1 * 0 + 1 * 0.5 + 1 * 1 = 1.5 입니다.
이런 우리가 원하는 z값은 0과 1사이의 값인데 1.5가 나왔습니다. 아~ 입력값과 가중치를 곱해서 모두 더하면 1을 넘는 값이 나올 수 있군요. 우리가 원하는 것은 0또는 1이므로 이것을 변환해주는 함수가 필요하겠습니다. 이러한 함수중 하나가 스텝 함수 입니다.

계산값 1.5는 0보다 크므로 스텝함수는 1을 반환합니다.
이처럼 입력과 가중치를 곱해서 나온 값을 입력으로 받아서 변환해주는 함수를 Activation Function이라고 합니다.
Inspired
퍼셉트론은 사람 뇌의 신경세포에서 영감을 받아 만든 것입니다. 그래서 아래의 신경세포 구조와 퍼셉트론을 비교해보면 매우 유사한 것을 느끼 실 수 있습니다.
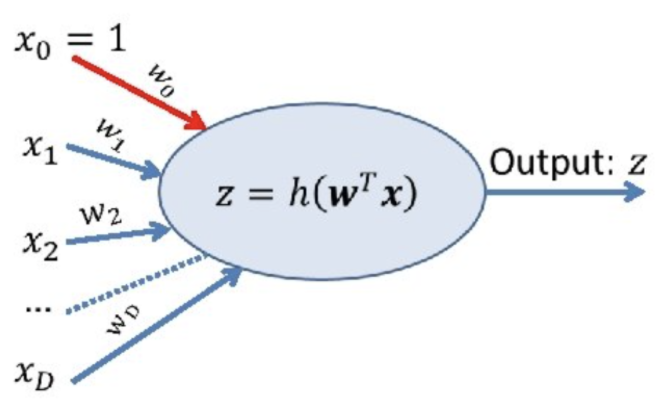
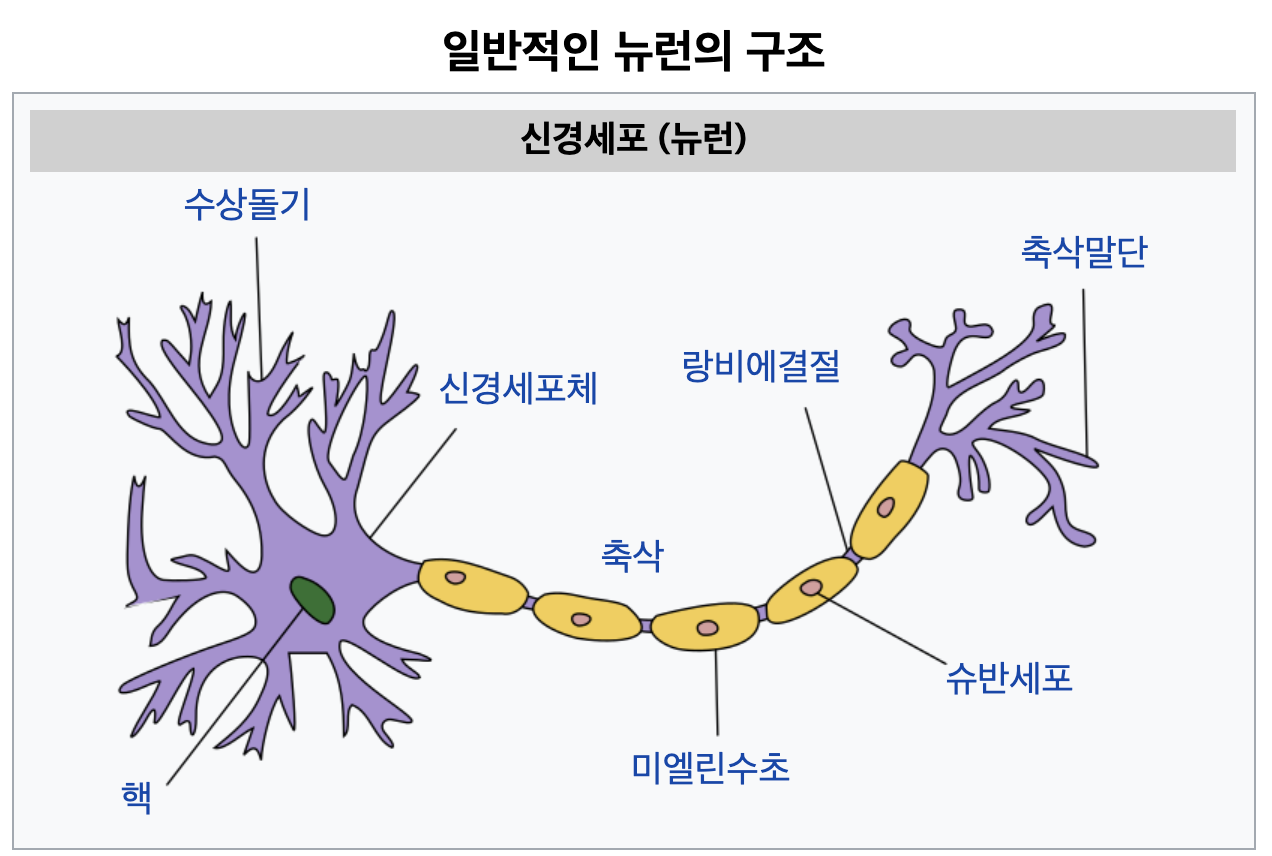
살짝 이상하게 들릴 수도 있지만 끼워 맞추어 보면, 수상돌기는 외부로부터의 자극을 받아들이는 기능으로 인풋 x와 같고, 핵은 첫번째 단계의 계산을 처리하는 곳으로 외부 입력과 가중치를 계산하는 곳 같고, 축삭은 처리된 자극을 다음 뉴런에게 전달할지 말지를 결정하는 것 같아서 두번째 단계의 계산을 처리하는 액티베이션 함수(Activation Function)와 같아 보입니다. 그리고 마지막으로 축삭 말단은 다음 뉴런으로 전달해주는 역할로 y 값이 되겠네요.
이러한 퍼셉트론은 여러개를 이어붙여서 다층 퍼셉트론(MLP)을 만들 수도 있습니다. 그 모양은 아래와 같이 딥러닝의 구조와 유사합니다. 딥러닝의 아버지라고 할까요?! ^^

소스
https://slidetodoc.com/neural-networks-part-1-introduction-cse-4309-machine/
Neural Networks Part 1 Introduction CSE 4309 Machine
Perceptrons and Neurons • Perceptrons are inspired by neurons. – Neurons are the cells forming the nervous system, and the brain. – Neurons somehow sum up their inputs, and if the sum exceeds a threshold, they "fire". • Since brains are "intelligen
slidetodoc.com
https://becominghuman.ai/multi-layer-perceptron-mlp-models-on-real-world-banking-data-f6dd3d7e998f
Multi layer Perceptron (MLP) Models on Real World Banking Data
A multi layer perceptron (MLP) is a class of feed forward artificial neural network. MLP consists of at least three layers of nodes: an…
becominghuman.ai
'인공지능-기계학습 > 통계_모델_알고리즘' 카테고리의 다른 글
| sklearn을 이용한 초간단 선형회귀 모델 (0) | 2022.08.25 |
|---|---|
| [차원축소/시각화 방법] TSNE - Python 에서 T-SNE를 이용하는 방법 (0) | 2022.07.25 |
| 최대가능도방법 MLE: Maximum Likelihood Estimation (0) | 2022.03.12 |
| 가능도/우도/Likelihood (0) | 2022.03.11 |
| 확률 밀도 함수 PDF (Probability Density Function) (0) | 2022.03.10 |