반응형
MRR: Mean reciprocal rank
Mean reciprocal rank (MRR) 은 랭킹 모델을 평가하기 위한 가장 간단한 방법중 하나 입니다. MRR은 질의(Q)에 대해 가장 적절한 아이템의 역순위 평균입니다. 역순위란 1을 제안된 리스트에서 적절한 아이템이 나타난 위치의 숫자로 나눈 것을 말합니다. 예를 보시면 쉽게 이해하실 수 있습니다.
| Query | Proposed Results | Correct response | Rank | Reciprocal rank |
| cat | catten, cati, cats | cats | 3 | 1/3 |
| torus | torii, tori, toruses | tori | 2 | 1/2 |
| virus | viruses, virii, viri | viruses | 1 | 1 |
Query 는 질의어/검색어이고, Proposed Results는 검색엔진의 결과로 제안된 내용입니다. Correc response는 질의어 입력시 우리가 원하는 제안 내용이고요, Rank는 결과에서 제안 내용이 위치한 순위 입니다. Reciprocal rank 는 1 나누기 Rank의 값 입니다. Mean Reciprocal rank 는 이러한 Reciprocal rank 를 평균한 값입니다. 이 내용을 공식으로 정리하면 아래와 같습니다.
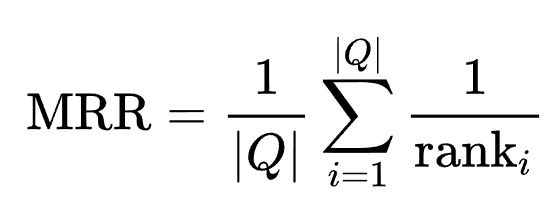
MRR = 1/|Q| Sigma i=1 to |Q| 1/rank i
따라서, 위 예시에 대한 MRR을 구해보면 아래와 같습니다.
MRR= 1/3*(1/2+1/3+1/1)= 11/18 = 0.61111
MRR의 한계중 하나는 검색 결과 아이템들 중에 하나의 순위만 고려하고 다른 것의 순위들은 무시한다는 것입니다. 따라서, 웹페이지에서 검색 결과를 중요도 순으로 노출하는 것에 대한 성능을 측정하고자 할 경우 MRR은 좋은 지표가 아닙니다. 여러 개의 위치와 중요성을 고려하지 못하기 때문이지요.
Precision at k
Precision at k (P@k) 는 많이 사용되는 또 다른 지표중 하나 입니다. 이 지표는 상위 k개의 문서중에서 연관된 문서의 수로 정의 됩니다.

예를 들면, 구글에서 “손 소독제” 를 검색한다고 생각해보겠습니다. 검색 결과 처음 페이지에 나온 10개 문서중에서 8개가 '손 소독제'와 연관된 문서라면 Precision@10(P@10)은 8/10 = 0.8 입니다.
여러 질의들 Q에 대한 Precision@k를 찾기 위해서는 Q에 있는 각 질문들에 대한 P@k의 평균 값으로 계산할 수 있습니다.
P@k는 몇가지 한계점이 있습니다.
가장 중요한 것은 상위 k개 연관된 문서들의 위치를 고려하지 못한다는 것 입니다. 이것은 매우 중요할 수 있습니다. 첫페이지에서 첫번째 문서가 연관된 문서일 경우와 첫페이지에서 마지막 문서가 연관된 문서일 경우는 완전히 다를 수 있습니다. (왜냐하면 첫페이지의 마지막 문서는 실제로 사용자가 보지 못할 수 있기 때문이지요.) 반면에 상위 k개의 결과들이 연관된 문서인지 아닌지만 검토하면 되기 때문에 모델을 쉽게 평가할 수 있습니다.
매우 비슷한 방법으로 정의되면서, 많이 사용되는 평가지표가 바로 recall@k입니다.
AP@k
AP@k(Average Precision at k). 앞에서 말씀드린 것처럼 Precision@K에서는 순서를 고려하지 않은 단점이 있었습니다. AP@K는 위치를 고려한 평가 지표입니다. 이말은 추천 리스트중에 높은 위치에 추천한 항목이 더 관심있는 항목으로 해야 좋다라는 가정에서 평가하는 방법입니다. 일반적으로 가정이 맞는 상황이지요. 공식은 아래와 같습니다. rel(i)는 선호 여부로 0 또는 1입니다.

Recall@k
Recall@k(R@k)는 검색 결과로 가져온 k개의 문서들 중에서 얼마나 많은 (적합한) 관련 문서가 있는 가로 계산할 수 있습니다. 즉, Recall@10의 경우, 가져온 10개의 문서중에서 8개가 관련된 문서이고 전체 관련 문서수가 9개인 경우 Recall@10은 8/9입니다.

Precision@k의 경우 가져온 문서 중에서 얼마나 정확한 문서가 많은 가를 중심으로 판단하는 지표라면, Recall@k는 가져와야할 문서 중에서 얼마나 많은 문서를 가져왔는가를 중심으로 판단하는 지표 입니다. 둘다 단점으로는 가져온 위치/순위를 고려하지 못한다는 것 입니다.
nDCG(CG/DCG/nDCG)
nDCG는 랭킹 시스템의 학습을 평가하기위해 가장 많이 사용되는 평가지표 입니다. 이전의 평가 지표들과는 달리 nDCG는 문서의 순서와 관련성의 중요성을 고려한 지표입니다. 즉, 추천 리스트의 위쪽에 관련성이 높은 문서가 위치할 수록 높은 값을 갖습니다.
nDCG의 공식적인 정의를 말하기 전에 먼저 두가지 연관 지표에 대해서 소개해 드리겠습니다. 바로 Cumulative Gain (CG) 과 Discounted Cumulative Gain (DCG) 입니다.
Cumulative Gain (CG) 이란 질의 결과로 가져온 각 문서의 연관성 점수를 모두 합친 것을 말합니다. 아래와 같이 정의될 수 있습니다.

여기에서는 각 문서의 연관성 점수(보통 상수)는 주어진다고 가정합니다.
Discounted Cumulative Gain (DCG) 는 CG에 가중치가 부여된 버전입니다. 결과의 위치에 따른 연관성 점수를 적절하게 변환하고자 로그함수를 사용합니다. 이것은 시스템의 성능을 평가할때 상당히 유용한데, 왜냐하면 처음 몇개의 문서들이 좀더 높은 가중치를 갖게되기 때문입니다. 검색 결과의 상위에 노출되는 결과 일수록 더 높은 가중치를 준다는 말은 검색 결과를 평가하는 입장에서 보면 맞는 말인 것 같습니다. DCG는 아래와 같이 정의 됩니다.

분모에 로그가 있어서 순서(i)가 커질 수록(추천 리스트의 아래에 위치할 수록) 분모가 커지면 DCG값은 작아집니다. 숫자가 많이 커져도 분모에 로그를 취하기 때문에 단순히 위치로 나눈 값보다는 적당히 커진 분모값이 됩니다.
또 다른 버전도 있습니다.
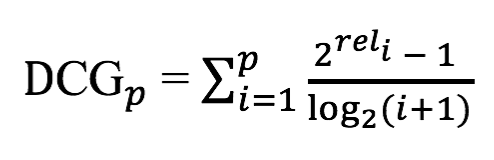
Normalized Discounted Cumulative Gain (NDCG) 는 실제 어플리케이션 평가에 더 적합하도록 DCG를 향상시켜서 고안된 것입니다. 가져온 문서들의 집합은 질의나 시스템에 따라 매우 다르기 때문에 nDCG는 DCG의 졍규화된 버전을 이용해서 성능을 평가합니다. 이상적인 시스템의 DCG로 평가하려는 시스템의 DCG를 나누는 것 입니다. 다른 말로 하면, 관련성을 기준으로 리스트 결과를 정렬하고, 해당 위치에서 이상적인 시스템에서 얻어지는 가장 좋은 DCG를 가지고 정규화하는(나누는) 것입니다.

여기서 IDCG는 “ ideal discounted cumulative gain”이고, 아래와 같이 정의합니다.

nDCG는 인기 많은 평가지표 입니다. 그러나 한계성도 있습니다. 주요 한계중 하나는 검색 결과 중에서 잘못된(연관성 없는) 문서를 가져온 것에 대한 패널티가 없다는 것 입니다. 이 말은 몇 개의 괜찮은 결과를 만드는 질의의 성능을 측정하는 것에 적합하지 않습니다. 특히, 검색 결과로 처음에 나오는 몇 개에만 관심이 있는 경우에는 더욱 적합하지 않습니다.
반응형
'인공지능-기계학습 > 평가지표_Metrics' 카테고리의 다른 글
| ML Metrics - Precision@k, Recall@k, MAP (0) | 2022.02.25 |
|---|---|
| ML 머신러닝 실무 - ML Metrics: Confusion Matrix - Accuracy, Precision, Recall, F1-scor (0) | 2022.02.17 |