다항분포 나이브 베이지안 분류-이해하기 쉽게
Naive Bayers Classification 나이브 베이지안 분류에는 크게 3가지로 가우시안, 다항분포, 베르누이(이항분포)가 있다.
이중에서 분류의 목적과 데이터 유형에 따라서 사용할 방법을 선택할 수 있다.
이번에는 다항분포 나이브 베이지안 분류에 대해서 알아보자.
비연속적인 데이터 값에 대해서 여러가지의 분류중에서 선택/분류하는 방법이다.
가장 많이 알려진 예시가 바로 스팸 메일 분류다. 즉, 메일의 제목과 내용을 보고 이 메일이 스팸 메일일지 아니면 정상적인 메일일지를 분류하는 알고리즘에 사용할 수 있다. 이러한 방법은 기계학습 방법중에서 지도학습(Supervised Learning)에 해당한다.
한번 생각해보자. 아래의 내용은 메일에 들어있는 내용을 단어로 표시한 것이다. 1번과 2번의 메일 중 어느 것이 스팸 메일 일까?
1번: 광고 출시 기념 할인 대상 선물 대박 핸드폰
2번: 회의 사장 회사 오전 대표님 연락 메일 예약 출시
당신은 몇번을 선택했나? 왜 그렇게 선택했나?
내 생각에는 1번이 스팸 메일 일 꺼라고 선택했는데, 이유는 1번에 나오는 단어들이 스팸 메일에서 자주 보이는 단어이기 때문이다.
이처럼 각 단어가 스팸 메일에서 나타나는 확률을 계산하고 모든 단어의 확률을 더해서 하나의 메일이 스팸 확률을 계산하는 방법이 바로 다항분포 베이지안 분류 방법이다.
다항분포 나이브 베이지안 알고리즘의 공식을 이해하기 쉽게 풀어서 상세하게 설명하겠다.
(아래 위키 페이지의 내용을 기반으로 설명)
나이브 베이즈 분류 - 위키백과, 우리 모두의 백과사전
기계 학습분야에서, '나이브 베이즈 분류(Naïve Bayes Classification)는 특성들 사이의 독립을 가정하는 베이즈 정리를 적용한 확률 분류기의 일종으로 1950 년대 이후 광범위하게 연구되고 있다. 통계
ko.wikipedia.org
먼저 간단한 공식 읽는 방법을 이해해 보자

p 는 확률을 말하고, w는 단어, i는 순서를 표시하고, C는 클래스를 말한다. 즉 풀어서 말하면 C라는 클래스에서 단어 wi가 나타날 확률이다. 실제 계산하는 방법은, 모든 C클래스에 속하는 단어의 출현 횟수 중에서 wi가 얼마나 나타났는지 계산하면 된다.(짧게 말하면, C클래스에 나타난 wi 출현 건수 / C클래스에 나타난 모든 단어 출현수 = wi 가 C클래스라는 조건에서 나타날 확률)
예를 들면, p(광고 | 스팸메일) 의 의미는
스팸메일이라는 클래스 조건에서 광고라는 단어가 나올 확률을 말한다.
그래서 우리는 C 클래스가 주어졌을때 D라는 문서가 나타날 확률을 아래와 같이 공식으로 만들 수 있다.

이 공식[공식2]을 풀어서 설명하면
C클래스(스팸메일)에 대하여 D(메일)이 속할 확률은 = C클래스(스팸메일)라는 조건에서 D의 각 단어(wi)가 나타날 확률을 모두 구하고 이 확률 들을 누적곱한 것
이다.
이처럼 [공식2]를 말하는 이유는 계산 할 수 있는 값 이기 때문이다. 즉, 스팸메일로 분류된 메일들의 내용을 통해서 스팸메일에 할당된 문서들의 워드 별로 스팸 메일에서의 출현 확률을 계산해 낼 수 있기 때문이다.
그런데 우리가 원하는 확률 값은 (새로운 메일 문서)D가 주어졌을때 C(스팸)일 확률이다.
수식으로는

이다
[공식2] 에서와 같이 만들 수 있지만 문제는 D라는 조건에서의 C클래스에 모든 단어가 출현할 확률을 계산할 수 없다. 왜냐하면 우리는 어떤 D가 들어올지 모르기 때문이다. 모든 단어 조합에 해당하는 D를 만들면 해당 문서가 C클래스에 속할 확률을 알 수 있겠지만 모든 단어 조합의 문서를 만든다는 말은 결국 무한대에 가깝기 때문에 만들 수 없다.
그런데 다행히도 우리는 아래의 조건부 확률 공식을 이용해서 공식을 바꿀 수 있다.

[공식4]를 이용하여 [공식3]을 아래와 같이 바꿀 수 있다.

이와 같은 방법으로 반대도 알 수 있다.

[공식6]을 이용해서 공식 5의 오른 쪽 분자에 있는 p(D ∩ C)를 p(C) p(D|C) 로 아래와 같이 바꿀 수 있다.

우리는 이공식을 공식2에 의해서 아래와 같이 바꿀 수 있다.


그런데 우리는 아직도 p(D)를 계산할 수가 없고
이렇게 계산해서 나온다고해도 그냥 클래스에 속할 확률인 값만 나온다. 예를 들면, 스팸 메일일 확률 88.833%, 일반 메일일 확률 88.799%. 이렇게 나와서 판단 하기 어렵다.
그래서 간단하게 스펨과 일반 두가지의 클래스만 있다고 가정하고 위 공식의 C를 스팸(S)과 일반(-S)로 바꾸면 아래와 같다.

결국 스팸 가능성이 더 큰지, 아니면 일반일 가능성이 더 큰지를 비교하면 되므로 계산해서 나온 두 값을 비율로 만들어서 어느 것이 더 높은지 판단 할 수 있다. 이를 위해 위의 공식 2개를 비율로 만들면 아래와 같다. 같은 항의 값으로 나눈 것이다.

이것을 조금 더 보기 좋게 정리하면 아래와 같다.
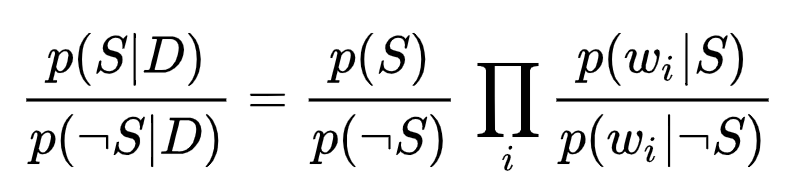
이렇게 계산하면 두 클래스간의 유서도비(우도비)율이 나오는데, 문제는 클래스에 속한 단어의 숫자가 일치하지 않고 발생 차이가 많이 날 수 있기 때문에 (예: 스팸단어 1,000개, 일반단어 100,000개) 로그를 취해서 크기/스케일을 맞추어 준다.

이렇게 해서 나온 값이 크면 스팸일 가능성이 높은 것이고 낮으면 일반 메일일 가능성이 높은 것이다. 이러한 구분/분류를 위해 테스트 데이터를 통해 적당한 기준값(Threshold)을 설정해 준다.
자, 이론도 알았으니 다음에는 이러한 나이브 베이지안 알고리즘을 이용하여 분류기를 직접 만들어 보자.